
已知一直角三角形的木板,三边的平方和为1800cm2,则斜边长为( )
A. 30cm B. 80cm C. 90cm D. 120cm
A 【解析】试题分析:设此直角三角形的斜边是c,根据勾股定理及已知不难求得斜边的长. 设此直角三角形的斜边是c, 根据勾股定理知,两条直角边的平方和等于斜边的平方. 所以三边的平方和即2c2=1800,c=±30(负值舍去),取c=30. 故选B.科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:填空题
如图,点E为等边△ABC中AC边的中点,AD⊥BC,且AD=5,P为AD上的动点,则PE+PC的最小值为________.
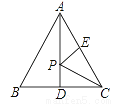
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2018届九年级上册期末模拟数学试卷 题型:填空题
已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣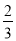 x2
x2
【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣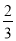 ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣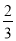 x2.
x2.
考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15
在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
12 【解析】试题解析:设口袋中白球可能有x个, ∵摸到红球的频率稳定在40%附近, ∴口袋中摸到红色球的概率为40%, ∴=40%, 解得:x=12, 故答案为12.查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:解答题
某产品生产车间有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获得利润100元,每生产一个乙种产品可获得利润180元.在这10名工人中,车间每天安排x名工人生产甲种产品,其余工人生产乙种产品.
(1)请写出此车间每天获取利润y(元)与x(人)之间的函数关系式;
(2)若要使此车间每天获取利润为14400元,要派多少名工人去生产甲种产品?
(3)若要使此车间每天获取利润不低于15600元,你认为至少要派多少名工人去生产乙种产品才合适?
【解析】 (1)根据题意得:y=12x×100+10(10﹣x)×180=﹣600x+18000。 (2)当y=14400时,有14400=﹣600x+18000,解得:x=6。 ∴要派6名工人去生产甲种产品。 (3)根据题意可得,y≥15600,即﹣600x+18000≥15600,解得:x≤4, ∴10﹣x≥6, ∴至少要派6名工人去生产乙种产品才合适。 ...查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:填空题
分解因式:x2y﹣y=______________.
y(x+1)(x﹣1) 【解析】试题分析:根据因式分解是把一个多项式化为几个因式积的形式.根据因式分解的一般步骤:一提(公因式)、二套(平方差公式,完全平方公式)、三检查(彻底分解),可得x2y﹣y=y(x2﹣1)= y(x+1)(x﹣1). 故答案为:y(x+1)(x﹣1)查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
如图1所示,将一个正四棱锥(底面为正方形,四条测棱相等)的其中四条边剪开,得到图2,则被剪开的四条边有可能是( )
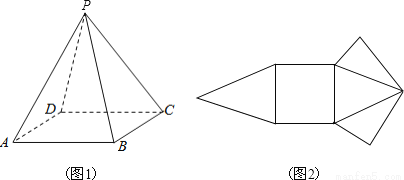
A. PA,PB,AD,BC B. PD,DC,BC,AB C. PA,AD,PC,BC D. PA,PB,PC,AD
A 【解析】由棱锥的展开特点知,被剪开的四条边有可能是PA,PB,AD,BC. 故选A.查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
点A,B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b﹣a<0;乙:a+b>0;丙:|a|<|b|;丁:ab>0,其中正确的是( )
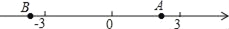
A. 甲、乙 B. 丙、丁 C. 甲、丙 D. 乙、丁
C 【解析】试题解析: 甲正确. 乙错误. 丙正确. 丁错误. 故选C.查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上期末模拟数学试卷 题型:单选题
下列各图中,可以是一个正方体的平面展开图的是( )
A. 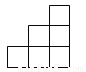 B.
B. 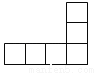 C.
C. 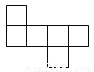 D.
D. 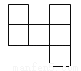
查看答案和解析>>
科目:初中数学 来源:2017年天津市中考数学模拟试卷(1) 题型:填空题
若a+3b﹣2=0,则3a•27b= .
9. 【解析】试题分析:根据幂的乘方运算以及同底数幂的乘法运算法则得出即可. 【解析】 ∵a+3b﹣2=0, ∴a+3b=2, 则3a×27b=3a×33b=3a+3b=32=9. 故答案为:9.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com