
如图,下列条件中,不能证明△ABD≌△ACD的是( )
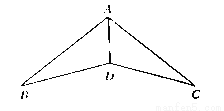
A. BD=DC ,AB=AC B. ∠ADB=∠ADC,∠BAD=∠CAD
C. ∠B=∠C, BD=DC D. ∠B=∠C ,∠BAD=∠CAD
C 【解析】试题解析:A、BD=DC,AB=AC,再加公共边AD=AD可利用SSS定理进行判定,故此选项不合题意; B、∠ADB=∠ADC,BD=DC再加公共边AD=AD可利用SAS定理进行判定,故此选项不合题意; C、∠B=∠C,BD=CD,再加公共边AD=AD不能判定△ABD≌△ACD,故此选项符合题意; D、∠B=∠C,∠BAD=∠CAD再加公共边AD=AD可利用AA...科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:解答题
某公司在销售一种产品进价为10元的产品时,每年总支出为10万元(不含进货支出).经过若干年销售得知,年销售量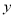 (万件)是销售单价
(万件)是销售单价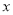 (元)的一次函数,并得到如下部分数据:
(元)的一次函数,并得到如下部分数据:
销售单价 | 12 | 14 | 16 | 18 |
年销售量 | 7 | 6 | 5 | 4 |
(1)求出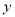 关于
关于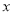 的函数关系式;
的函数关系式;
(2)写出该公司销售这种产品的年利润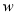 (万元)关于销售单价
(万元)关于销售单价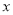 (元)的函数关系式;当销售单价
(元)的函数关系式;当销售单价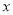 为何值时,年利润最大?
为何值时,年利润最大?
(3)试通过(2)中的函数关系式及其大致图象,帮助该公司确定产品的销售单价范围,使年利润不低于20万元(请直接写出销售单价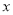 的范围).
的范围).
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
若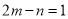 ,则多项式
,则多项式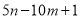 的值是_________.
的值是_________.
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
计算下列各题
(1)(-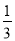 )-2+(2018-π)0-(-3)2
)-2+(2018-π)0-(-3)2
(2)(2x+y)2+(x+y)(x-y)-5x(x-y)
(1)1;(2)9xy 【解析】试题分析:(1)按照有理数混合运算的顺序,先乘方后乘除最后算加减,有括号的先算括号里面的. (2)按照完全平方公式、平方差公式和单项式乘以多项式的运算法则把括号去掉,再合并同类项即可求出结果. 试题解析:(1)原式=9+1-9=1; (2)原式=4x2+4xy+y2+x2-y2-5x2+5xy =9xy.查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
若分式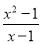 的值为0,则
的值为0,则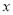 的值为( )
的值为( )
A. -1 B. 1 C. 1 D. 不等于1的数
A 【解析】试题解析:∵分式的值为0, ∴x2-1=0,x-1≠0, 解得:x=-1. 故选A.查看答案和解析>>
科目:初中数学 来源:安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型:解答题
已知关于x的一元二次方程为:x2+2x+2k-4=0.
(1)当方程有两实数根时,求k的取值范围;
(2)任取一个k值,求出方程的两个不相等实数根.
(1)k≤;(2) , . 【解析】(1)根据一元二次方程的根的判别式,建立关于k的不等式,求出k的取值范围; (2)先确定k=1或2,再根据方程的根都是整数,可知20-8k是完全平方数,即可求k的值. 【解析】 (1)关于x的一元二次方程x2+2x+2k-4=0中, ∴a=1,b=2,c=2k-4, ∵方程有两个不相等的实数根, ∴△=b2-4ac=20-8k>0, ∴k...查看答案和解析>>
科目:初中数学 来源:安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型:填空题
已知扇形的面积为12πcm2,半径为12cm,则该扇形的圆心角是_______.
30° 【解析】设圆心角为n°,由题意得: =12π, 解得:n=30, 故答案为:30°.查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:解答题
如图,Rt△ABC中, 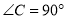 ,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为
,AC=BC,AB=4cm.动点D沿着A→C→B的方向从A点运动到B点.DE⊥AB,垂足为E.设AE长为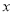 cm,BD长为
cm,BD长为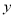 cm(当D与A重合时,
cm(当D与A重合时, 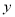 =4;当D与B重合时
=4;当D与B重合时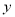 =0).
=0).
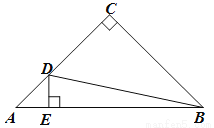
小云根据学习函数的经验,对函数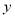 随自变量
随自变量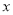 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小云的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了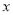 与
与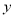 的几组值,如下表:
的几组值,如下表:
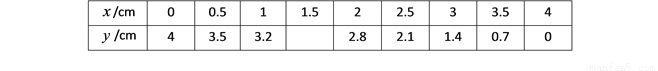
补全上面表格,要求结果保留一位小数.则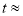 __________.
__________.
(2)在下面的网格中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题:当DB=AE时,AE的长度约为 cm.
(1)2.9;(2)答案见解析;(3)2.3. 【解析】试题分析:(1)通过取点、画图、测量,可得到结果; (2)通过描点,连线即可作出函数的图象; (3)根据题意可得当DB=AE时,AE的长度约为2.3cm. 试题解析:(1)2.9 (2)如图所示: (3)2.3查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:填空题
请写出一个开口向上,并且与y轴交于点(0,2)的抛物线的表达式:_________.
.(答案不唯一) 【解析】∵抛物线开口向上, ∴a>0. ∵抛物线与y轴交于点(0,2), ∴c=2, ∴抛物线解析式可以是:y=x2+2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com