
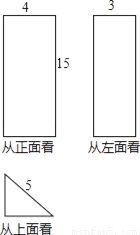
��ͼ��ʾ����ij������������ֲ�ͬ������������ͼ�Σ�
��1��˵���������ͼ�ε����ƣ�
��2������ͼ�е��й����ݣ������������ı�����������
 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�����������������2017���п���ѧһģ�Ծ� ���ͣ������
��ͼ��AB�ǡ�O���ң�OP��OA��AB�ڵ�P������B��ֱ�߽�OP���ӳ����ڵ�C����CP=CB��
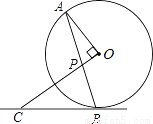
��1����֤��BC�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ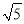 ��OP=1����BC�ij���
��OP=1����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ���ѡ��
��ƽ��ֱ������ϵ�У��㣨1����2������ԭ��ԳƵĵ�������ǣ� ��
A����1��2�� B������1��2�� C����2����1�� D����2��1��
B �������� ���������ƽ��ֱ������ϵ������һ��P��x��y��������ԭ��ĶԳƵ��ǣ�-x��-y�����ɵõ㣨1��-2������ԭ��ԳƵĵ�������ǣ�-1��2���� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶����ĩģ����ѧ�Ծ������𰸣� ���ͣ������
�ֽ���ʽ��a3��ab2=�� ����
�����������������a3-ab2=a��a2-b2��=a��a+b����a-b�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����꼶����ĩģ����ѧ�Ծ������𰸣� ���ͣ���ѡ��
�������ʽ��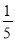 abc+
abc+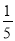 ab2��a2bc��һ����ʽ�ǩ�
ab2��a2bc��һ����ʽ�ǩ�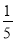 ab����ô��һ����ʽ�ǣ�������
ab����ô��һ����ʽ�ǣ�������
A. c��b+5ac B. c+b��5ac C. c��b+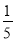 ac D. c+b��
ac D. c+b��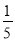 ac
ac
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ ������÷� ���ͣ������
��2015��•��������ĩ����ͼ��ֱ��y=k1x+b�뷴��������y=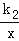 ��x��0����ͼ����A��1��6����B��a��3�����㣮
��x��0����ͼ����A��1��6����B��a��3�����㣮
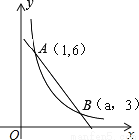
��1����k1��k2��ֵ��
��2�����ͼ��ֱ��д��k1x+b�� ��0��x��ȡֵ��Χ��
��0��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ ������÷� ���ͣ������
��Rt��POQ�У�OP=OQ=4��M��PQ�е㣬��һ���dzߵ�ֱ�Ƕ�����ڵ�M������MΪ��ת���ģ���ת���dzߣ����dzߵ���ֱ�DZ����POQ����ֱ�DZ߷ֱ��ڵ�A��B��
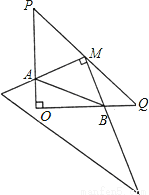
��1����֤��MA=MB��
��2������AB��̽��������ת���dzߵĹ����У���AOB���ܳ��Ƿ������Сֵ�������ڣ������Сֵ���������ڣ���˵�����ɣ�
��1��֤������������2������Сֵ����СֵΪ4+2�� �������� �����������1������M��ME��OP�ڵ�E����MF��OQ�ڵ�F���ɵ��ı���OEBF�Ǿ��Σ����������ε���λ�߶����ɵ�ME=MF���ٸ���ͬ�ǵ������ȿɵá�AME=��BMF�������á��DZ߽ǡ�֤����AME�͡�BMFȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ���֤���� ��2������ȫ�������ζ�Ӧ����ȿɵ�AE=BF����OA=x����ʾ��AEΪ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭������������ʮ����ѧ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
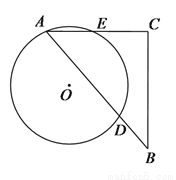
��ͼ��һ�麬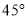 �ǵ�ֱ�����ǰ壬����һ����Ƕ���
�ǵ�ֱ�����ǰ壬����һ����Ƕ���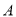 �ڰ뾶Ϊ
�ڰ뾶Ϊ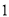 �ġ�
�ġ�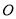 �ϣ���
�ϣ���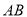 ��
�� 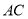 �ֱ����
�ֱ����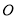 ���ڵ�
���ڵ�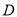 ��
��  ����
���� �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С����÷� ���ͣ������
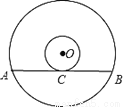
��ͼ����һ�ŵ��Թ��̵ı��棬����Բ�Ķ���O����Բ����AB���ڵ�ֱ����СԲ�����ߣ��е�ΪC����֪��Բ�İ뾶Ϊ5cm��СԲ�İ뾶Ϊ1cm������AB�ij��� ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com