练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：|a|=2，|b|=3且a＞b，求a+b的值．

    －1或－5． 【解析】试题分析：计算绝对值要根据绝对值的定义求解，注意在条件的限制下a，b的值剩下2组． 【解析】 ∵|a|=2，|b|=3， ∴a=±2，b=±3． ∵a＞b， ∴当a=2时，b=﹣3，则a+b=﹣1． 当a=﹣2时，b=﹣3，则a+b=﹣5．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省2017-2018学年七年级上期末模拟数学试卷 题型：填空题

    如果“□×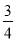（﹣）=1”，则□内应填的实数是________．

    【解析】试题解析：1÷（-）=1×（-）=-， 则□内应填的实数是-．

    查看答案和解析>>

    科目：初中数学 来源：甘肃省张掖市高台县2016-2017学年八年级（上）期末数学试卷 题型：解答题

    如图，AD=CD，AC平分∠DAB，求证：DC∥AB．

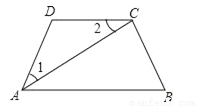
    证明见解析． 【解析】试题分析：由等腰三角形的性质和角平分线的定义可求得∠2=∠BAC，再根据平行线的判定可得出结论． 试题解析：证明：∵AD=CD， ∴∠1=∠2， ∵AC平分∠DAB， ∴∠1=∠BAC， ∴∠2=∠BAC， ∴DC∥AB．

    查看答案和解析>>

    科目：初中数学 来源：甘肃省张掖市高台县2016-2017学年八年级（上）期末数学试卷 题型：单选题

    下列命题是真命题的是（　　）

    A. 互补的两角相等，则这两角都是直角

    B. 直线是平角

    C. 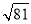的算术平方根是9

    D. 不相交的两条直线叫做平行线

    A 【解析】试题解析：A. 互补的两角相等，则这两角都是直角.是真命题. B.直线不是直角.是假命题. C. 的算术平方根是3.是假命题. D. 在同一平面内，不相交的两条直线叫做平行线.是假命题. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级上期末复习检测数学试卷 题型：解答题

    先化简，再求值：3x（x﹣2y）﹣[3x2﹣2y+2（xy+y）]，其中x=﹣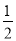，y=﹣3．

    ﹣8xy，﹣12． 【解析】试题分析：首先根据去括号的法则将括号去掉，然后进行合并同类项，最后将x和y的值代入化简后的式子进行计算得出答案． 试题解析：原式=， 当x=，y=-3时，原式=-8×()×(-3)=-12．

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级上期末复习检测数学试卷 题型：填空题

    计算：﹣3+（﹣4）=________

    -7 【解析】﹣3+（﹣4）=﹣（3+4）=﹣7， 故答案为：﹣7．

    查看答案和解析>>

    科目：初中数学 来源：山东省2017-2018学年七年级上期末复习检测数学试卷 题型：单选题

    若x=1是关于x的方程ax+1=2的解，则a是（ ）

    A. 1 B. 2 C. -1 D. -2

    A 【解析】分析：首先由已知把x=1代入ax+1=2得到关于a的方程，然后解方程求出a． 解答：【解析】 把x=1代入ax+1=2得： a+1=2， 解得：a=1． 故答案为：A．

    查看答案和解析>>

    科目：初中数学 来源：重庆市江北区2018届九年级上期末模拟数学试卷 题型：填空题

    如图，直线l与半径为4的⊙O相切于点A，P是⊙O上的一个动点（不与点A重合），过点P作PB⊥l，垂足为B，连接PA．设PA=x，PB=y，则（x﹣y）的最大值是________．

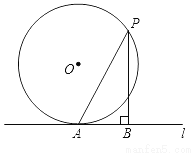
    2 【解析】试题分析：∵AC是直径，∴∠CPA=90°，又∵AB是切线，∴CA⊥AB， ∵PB⊥l，∴AC∥PB，∴∠CAP=∠APB，∴△APC∽△PBA，∴=， ∴=，∴y=x2，∴x﹣y=x﹣x2=﹣x2+x=﹣（x﹣4）2+2， 因此当x=4时，x﹣y有最大值是2，

    查看答案和解析>>

    科目：初中数学 来源：2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型：解答题

    如图，在平面直角坐标系中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=1，OC=2，点D在边OC上且OD=1.25．

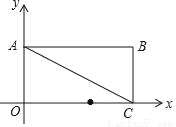
    （1）求直线AC的解析式．

    （2）在y轴上是否存在点P，直线PD与矩形对角线AC交于点M，使得△DMC为等腰三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

    （3）抛物线y=﹣x2经过怎样平移，才能使得平移后的抛物线过点D和点E（点E在y轴正半轴上），且△ODE沿DE折叠后点O落在边AB上O′处？

    （1） ；（2）P点坐标为（0， ）或（0，﹣）或（0， ）或（0， ）； （3）抛物线y=﹣x2先向右单位，再向上平移单位，才能使得平移后的抛物线过点D和点E． 【解析】试题分析：（1）先确定点和点坐标，然后利用待定系数法求直线的解析式； （2）设讨论：当时， 解方程求出，再求出的解析式，从而得到点坐标；当时，易得点的坐标，接着求出的解析式，从而得到点坐标；当CM=CD时, 解方程求出，...

    查看答案和解析>>

    同步练习册答案