
��ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA��y����������ϣ�OC��x����������ϣ�OA=1��OC=2����D�ڱ�OC����OD=1.25��
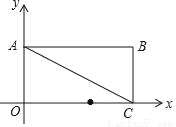
��1����ֱ��AC�Ľ���ʽ��
��2����y�����Ƿ���ڵ�P��ֱ��PD����ζԽ���AC���ڵ�M��ʹ�á�DMCΪ���������Σ������ڣ�ֱ��д�����з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��3��������y=��x2��������ƽ�ƣ�����ʹ��ƽ�ƺ�������߹���D�͵�E����E��y���������ϣ����ҡ�ODE��DE�۵����O���ڱ�AB��O�䴦��
��1�� ����2��P������Ϊ��0�� ����0��������0�� ����0�� ���� ��3��������y=��x2�����ҵ�λ��������ƽ�Ƶ�λ������ʹ��ƽ�ƺ�������߹���D�͵�E�� �������������������1����ȷ����͵����꣬Ȼ�����ô���ϵ������ֱ�ߵĽ���ʽ�� ��2�������ۣ���ʱ�� �ⷽ�������������Ľ���ʽ���Ӷ��õ������ꣻ��ʱ���õ�����꣬��������Ľ���ʽ���Ӷ��õ������ꣻ��CM=CDʱ, �ⷽ�������... ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��ɽ��ʡ2017-2018ѧ�����꼶����ĩ��ϰ�����ѧ�Ծ� ���ͣ������
��֪��|a|=2��|b|=3��a��b����a+b��ֵ��
��1��5�� ������������������������ֵҪ���ݾ���ֵ�Ķ�����⣬ע����������������a��b��ֵʣ��2�飮 �������� ��|a|=2��|b|=3�� ��a=��2��b=��3�� ��a��b�� �൱a=2ʱ��b=��3����a+b=��1�� ��a=��2ʱ��b=��3����a+b=��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������н�����2018����꼶����ĩģ����ѧ�Ծ� ���ͣ���ѡ��
�������������y��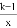 ��ͼ����(��1����2)����k��ֵ�� ( )
��ͼ����(��1����2)����k��ֵ�� ( )
A. 2 B. ��2 C. ��3 D. 3
D ��������������������⿼������ô���ϵ�������������Ľ���ʽ������ѧ�ε��ص㣮������ʱ�������ˡ�����������ͼ���ϵ��������������һ֪ʶ��.���ݷ���������ͼ���ϵ����������������-1��-2��������֪�����������Ľ���ʽ���г�����ϵ��k�ķ��̣�ͨ���ⷽ�̼������k��ֵ�� �������⣬�� -2=k?1?1����2=k-1�� ��ã�k=3�� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ������� ���ͣ������
ʹ����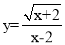 �������x��ȡֵ��Χ��_____��
�������x��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ���п���ѧģ���Ծ������� ���ͣ���ѡ��
��ͼֱ��a��b������DC��ֱ��a�ཻ�ڵ�C������D��DE��b�ڵ�E����֪��1��25�㣬���2�Ķ���Ϊ( )
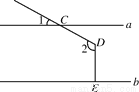
A. 115�� B. 125�� C. 155�� D. 165��
A ���������������������D��DF��a�����CDF=��1=25�㣬��FDE=90�㣬���2=25��+90��=115��.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�������������˻�ʵ��ѧУ�п���ѧģ���Ծ� ���ͣ������
��ͼ����ij����������У���Ա�״����ŵײ����ĵ�O����ǰ��10m��������ţ������������߷������������ߣ�������������߶�Ϊ3mʱ�ﵽ��ߵ㣬��ʱ������е�ˮƽ����Ϊ6m����֪���ŵĺ�����Ϊ2.44m��
��1������ͼ��ʾ��ƽ��ֱ������ϵ�У��ʴ˷��������ܷ�����ţ����������������
��2������Ա��վ�ھ�������2m����������ʱ�ֵ��������Ϊ2.52m��������ֹ��Ա�Ĵ˴�������������ܣ������ٺ��˶�Զ������ֹ��Ա�����ţ�
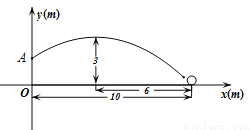
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�������������˻�ʵ��ѧУ�п���ѧģ���Ծ� ���ͣ������
��ͼ��С���������ֱ�ǣ��������ӿ�DE��������AD=2m��BD=3m��CE=9m����ӿ�DEΪ_____m��
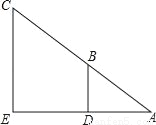
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��˳��2017-2018ѧ����꼶��ѧ����ĩ��ѧ���������ѧ�Ծ� ���ͣ������
�ⷽ�̣� 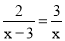
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
һԪ���η���x2=2x�ĸ���______��
2��0 ����������x2=2x�� ��x2?2x=0�� ��x(x?2)=0�� ��x=0��x?2=0�� ��һԪ���η���x2=2x�ĸ�x1=0��x2=2. �ʴ�Ϊ��2��0.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com