
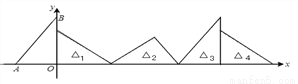
如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作翻转变换,依次得到△1、△2、△3、△4…,则△23中的B23的坐标为_______________.
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:填空题
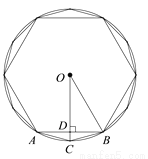
“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”这是我国古代著名数学家刘徽在《九章算术注》中提到的“如何求圆的周长和面积”的方法,即“割圆术”.“割圆术”的主要意思是用圆内接正多边形去逐步逼近圆.刘徽从圆内接正六边形出发,将边数逐次加倍,并逐次得到正多边形的周长和面积.如图,AB是圆内接正六边形的一条边,半径OB=1,OC⊥AB于点D,则圆内接正十二边形的边BC的长是_________________(结果不取近似值).
查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:解答题
如图,已知△ABC中,点D、E分别在边AB和AC上,DE∥BC,且DE经过△ABC的重心,设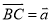 .
.
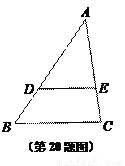
(1)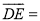 (用向量
(用向量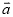 表示);
表示);
(2)设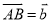 ,在图中求作
,在图中求作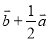 .
.
(不要求写作法,但要指出所作图中表示结论的向量.)
(1);(2)详见解析. 【解析】试题分析:(1)由DE∥BC,DE经过△ABC的重心,可得AD:AB=DE:BC=2:3,即可求得; (2)取点BC的中点M,连接AM,则即为所求. 试题解析:(1)∵DE∥BC,DE经过△ABC的重心, ∴AD:AB=DE:BC=2:3,, ∵, ∴ ; (2)如图,取点AB的中点M,连接AM,则即为所求.查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:单选题
已知在Rt△ABC中,∠C=90°,AB=7,BC=5,那么下列式子中正确的是
A. 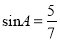 B.
B. 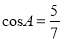 C.
C. 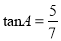 D.
D. 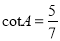
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:解答题
已知关于x的一元二次方程为:x2+2x+2k-4=0.
(1)当方程有两实数根时,求k的取值范围;
(2)任取一个k值,求出方程的两个不相等实数根.
(1)k≤;(2) , . 【解析】(1)根据一元二次方程的根的判别式,建立关于k的不等式,求出k的取值范围; (2)先确定k=1或2,再根据方程的根都是整数,可知20-8k是完全平方数,即可求k的值. 【解析】 (1)关于x的一元二次方程x2+2x+2k-4=0中, ∴a=1,b=2,c=2k-4, ∵方程有两个不相等的实数根, ∴△=b2-4ac=20-8k>0, ∴k...查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:填空题
方程(x+3)(x-2)=0的解是___________________.
, . 【解析】【解析】 (x+3)•(x﹣2)=0,∴x+3=0,x﹣2=0,解方程得:x1=2,x2=﹣3.故答案为:x1=2,x2=﹣3.查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:单选题
下列图形中既是中心对称图形,又是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
如图,已知∠1=∠2,则添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
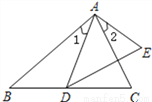
A. 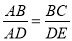 B.
B. 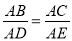 C. ∠B=∠ADE D. ∠C=∠E
C. ∠B=∠ADE D. ∠C=∠E
查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市宁城县2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
当三角形中一个内角α是另一个内角β的一半时,我们称此三角形为“半角三角形”,其中α称为“半角”.如果一个“半角三角形”的“半角”为25°,那么这个“半角三角形”的最大内角的度数为________.
105° 【解析】根据半角三角形的定义, “半角”α为25°,则另一个内角β=50°,根据三角形内角和定理可求出最大内角为: 105°,故答案为: 105°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com