练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

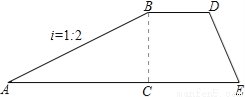
    如图是拦水坝的横断面，斜坡AB的水平宽度为12米，斜面坡度为1：2，则斜坡AB的长为 ．

    6 【解析】试题分析：根据斜面坡度为1：2，斜坡AB的水平宽度为12米，可得AC=12m，BC=6m，然后利用勾股定理求出AB的长度． 【解析】 ∵斜面坡度为1：2，AC=12m， ∴BC=6m， 则AB===（m）． 故答案为：6m．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型：填空题

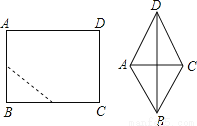
    如图，将一个长为10cm，宽为8cm的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到菱形的面积为______cm2．

    10 【解析】【解析】 矩形对折两次后，所得的矩形的长、宽分别为原来的一半，即为5cm，4cm，而沿两邻边中点的连线剪下，剪下的部分打开前相当于所得菱形的沿对角线两次对折的图形，所以菱形的两条对角线的长分别为5cm，4cm，所以．菱形的面积=4×5÷2=10cm2．故答案为：10．

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    （1）计算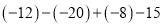： （2）计算：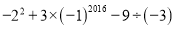

    （1）-15；（2）2 【解析】试题分析：（1）去括号进行加减运算即可；（2）先计算乘方，再对乘法除法进行运算，最后进行加减运算即可. 试题解析： 【解析】 （1）原式=－12+20－8－15=8－8－15=－15； （2）原式=－4+3×1+3=－4+3+3=－1+3=2.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型：解答题

    如图1，抛物线y=-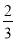x2+bx+c与x轴相交于点A，C，与y轴相交于点B，连接AB，BC，点A的坐标为（2，0），tan∠BAO=2，以线段BC为直径作⊙M交AB于点D，过点B作直线l∥AC，与抛物线和⊙M的另一个交点分别是E，F．

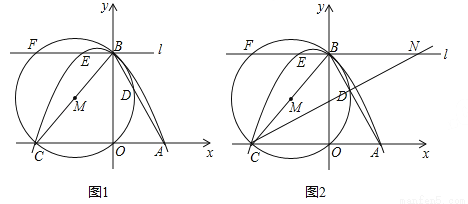
    （1）求该抛物线的函数表达式；

    （2）求点C的坐标和线段EF的长；

    （3）如图2，连接CD并延长，交直线l于点N，点P，Q为射线NB上的两个动点（点P在点Q的右侧，且不与N重合），线段PQ与EF的长度相等，连接DP，CQ，四边形CDPQ的周长是否有最小值？若有，请求出此时点P的坐标并直接写出四边形CDPQ周长的最小值；若没有，请说明理由．

    （1）抛物线的解析式为y=-x2-x+4．（2）2．（3）2+2+2． 【解析】 试题分析：（1）根据点A的坐标和tan∠BAO=2求得AO=2，BO=4，从而求得点B的坐标为（0，4），利用待定系数法求得二次函数的解析式即可． （2）首先根据抛物线的对称轴求得点A的对称点C的坐标，然后求得点B的对称点E的坐标为（-1，4），从而求得BE的长，得到EF的长即可； （3）作点...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型：解答题

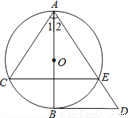
    如图，AB为⊙O的直径，劣弧BC=劣弧BE，BD∥CE，连接AE并延长交BD于D．

    求证：（1）AC=AE；

    （2）AB2=AC•AD．

    （1）证明见解析（2）证明见解析 【解析】试题分析：（1）由垂径定理的推论得出AB是CE的中垂线，所以AC=AE； （2）连接BC，证明△ACB∽△ABD，再利用相似三角形的性质即可得. 试题解析：（1）∵，AB为⊙O的直径， ∴AB垂直平分CE， ∴AE=AC； （2）连接BC， ∵ AB为⊙O的直径 ，∴∠ACB=90º， ∵ BD//CE，AB...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型：填空题

    正六边形的每个中心角为_________度．

    60 【解析】正六边形的圆心角等于一个周角，即为360° ，正六边形有6个中心角， 所以每个中心角=360°÷6=60°， 故答案为：60.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型：单选题

    若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根，则k的取值范围是（　　）

    A. k＞﹣1 B. k＞﹣1且k≠0 C. k＜1 D. k＜1且k≠0

    B 【解析】试题解析：∵关于x的一元二次方程kx2-2x-1=0有两个不相等的实数根， ∴k≠0且△＞0，即（-2）2-4×k×（-1）＞0， 解得k＞-1且k≠0． ∴k的取值范围为k＞-1且k≠0． 故选B.

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市蓬溪县2018届九年级上学期期末考试数学试卷 题型：填空题

    两个相似三角形周长的差是4cm，面积的比是16:25，那么这两个三角形的周长分别是__________cm和____________cm

    16 20 【解析】试题解析：∵两个相似三角形面积的比是16:25， ∴两个相似三角形周长比为4:5. 由题意，可设较小三角形的周长为4xcm，则较大三角形的周长为5xcm， 则有：5x-x=4，解得x=4， ∴这两个三角形的周长分别是16cm和20cm. 故答案为：16，20.

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年七年级上学期期末考试数学试卷 题型：解答题

    某班准备买一些乒乓球和乒乓球拍，先了解情况如下：甲、乙两家商店出售有同样品牌的乒乓球和乒乓球拍，乒乓球拍每副30元，乒乓球每盒定价5元，经洽谈后，甲店没卖一副球拍赠一盒乒乓球，乙店全部按定价的9折优惠，该班需球拍5副，乒乓球若干盒（不少于5盒）.

    (1)当购买多少盒乒乓球时，两种优惠办法付款一样？

    (2)当购买30盒乒乓球时，去哪家商店购买更划算？

    (3)当购买30盒乒乓球时，你有其它的更好的省钱方案吗？并计算费用。

    (1) 购买20盒乒乓球时，两种优惠办法付款一样.(2) 购买30盒乒乓球时，去乙店购买合算.(3) 247.5元. 【解析】试题分析:(1)设购买x盒乒乓球时,两种优惠办法付款一样,先根据两家的收费标准分别表示出费用,再令两种费用相等列出方程,求出方程的解即可得到结果, (2)根据(1)中的代数式,把x=30分别代入计算算出钱数即可, (3) 较好的方案是去甲商场购买5副乒乓球...

    查看答案和解析>>

    同步练习册答案