
若一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为( )
A. 90° B. 105° C. 130° D. 120°
C 【解析】试题分析:设出相应的边数和未知的那个内角度数,利用内角和公式列出相应等式,根据边数为整数求解即可. 设这个内角度数为x,边数为n, 则(n-2)×180°-x=2570°, 180°•n=2830°+x, ∵n为正整数, ∴n=18, ∴这个内角度数为180°×(18-2)-2570°=130°, 故选C. 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源:甘肃省张掖市2017-2018学年七年级(上)期中数学试卷 题型:单选题
用平面截一个正方体,所得截面不可能是( )
A. 等腰三角形 B. 长方形 C. 直角三角形 D. 梯形
C 【解析】截面经过正方体的三个面时,得到三角形,任意两条线断不可能垂直,所以,截面不可能是直角三角形, 故选C.查看答案和解析>>
科目:初中数学 来源:浙江省2017-2018学年八年级12月月考数学试卷 题型:填空题
如图,Rt△ABC中,∠ABC=90°,D为AC的中点,AC=10,则BD=________。
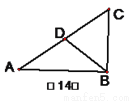
查看答案和解析>>
科目:初中数学 来源:福建省三明市大田县2017-2018学年八年级上期末模拟数学试卷 题型:解答题
如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.
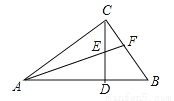
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
(1)证明见解析;(2)证明见解析. 【解析】 试题分析:(1)由于∠ACD与∠B都是∠BCD的余角,根据同角的余角相等即可得证; (2)根据直角三角形两锐角互余得出∠CFA=90°-∠CAF,∠AED=90°-∠DAE,再根据角平分线的定义得出∠CAF=∠DAE,然后由对顶角相等的性质,等量代换即可证明∠CEF=∠CFE. 试题解析:(1)∵∠ACB=90゜,CD⊥AB于...查看答案和解析>>
科目:初中数学 来源:福建省三明市大田县2017-2018学年八年级上期末模拟数学试卷 题型:填空题
如图,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有________个,它们分别是________.
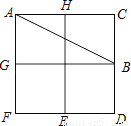
查看答案和解析>>
科目:初中数学 来源:福建省三明市大田县2017-2018学年八年级上期末模拟数学试卷 题型:单选题
小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长可以为( )
A. 3cm B. 4cm C. 9cm D. 10cm
C 【解析】试题分析:由题意可知,A项,3+3<7,故不符合题意;B项,3+4=7,故不符合题意;D项,3+7=10,故不符合题意;C项,3+9>7,符合题意,故选C项.查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市第一学期八年级数学期末复习综合检测卷 题型:解答题
如图,等边三角形 的边长为4,点
的边长为4,点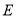 是边
是边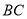 上一动点(不与点
上一动点(不与点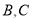 重合),以
重合),以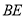 为边在
为边在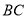 的下方作等边三角形
的下方作等边三角形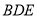 ,连接
,连接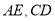 .
.
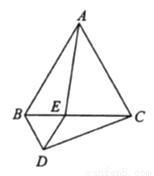
(1)在运动的过程中, 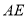 与
与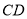 有何数量关系?请说明理由.
有何数量关系?请说明理由.
(2)当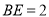 时,求
时,求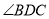 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市第一学期八年级数学期末复习综合检测卷 题型:单选题
一等腰三角形底边长为8 cm,腰长为5 cm,则腰上的高为( )
A. 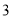 cm B.
cm B. 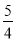 cm C.
cm C. 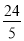 cm D.
cm D. 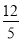 cm
cm
查看答案和解析>>
科目:初中数学 来源:江苏省实验学校2017-2018学年七年级上学期第二次月检测数学试卷 题型:填空题
把一根木条钉牢在墙壁上需要 ______ 个钉子,其理论依据是: ______ .
2 两点确定一条直线 【解析】试题分析:根据过同一平面上的两点有且只有一条直线,即两点确定一条直线,即可解题. 【解析】 把一根木条钉牢在墙壁上需要2个钉子; 其理论依据是:两点确定一条直线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com