练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列说法正确的是( )

    A. 过一点有且只有一条直线与已知直线垂直

    B. 从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离

    C. 在平面内，有且只有一条直线与已知直线垂直

    D. 直线a外一点M与直线a上各点连接而成的所有线段中最短线段的长是3cm，则点M到直线a的距离是3cm

    D 【解析】试题解析：A. 在平面内过一点有且只有一条直线与已知直线垂直，故原说法错误； B. 从直线外一点到这条直线的垂线段的长度，叫做这点到这条直线的距离，故原说法错误； C. 在平面内，过一点有且只有一条直线与已知直线垂直，故原说法错误； D. 直线a外一点M与直线a上各点连接而成的所有线段中最短线段的长是3cm，则点M到直线a的距离是3cm，正确.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省长沙市2017-2018学年九年级（上）第一次月考数学试卷 题型：单选题

    不等式组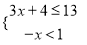的解集在数轴上表示正确的是（　　）

    A. 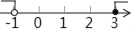B.

    C. D.

    D 【解析】试题分析：解不等式3x＋4≤13，得：x≤3， 解不等式﹣x＜1，得：x＞﹣1， 则不等式组的解集为﹣1＜x≤3， 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.1.1 相交线与平行线 同步练习 题型：单选题

    下列说法正确的是( )

    A．同一平面内没有公共点的两条线段平行

    B．两条不相交的直线是平行线

    C．同一平面内没有公共点的两条直线平行

    D．同一平面没有公共点的两条射线平行

    C 【解析】判断平行时，前提条件必须是在同一平面内，另外，线段和射线的平行，是指它们所在的直线平行，故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型：填空题

    如图，直线AB、CD、EF相交于点O，∠AOD＝150°，∠DOE＝80°，则∠AOF＝____.

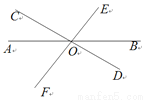
    50° 【解析】∵∠AOD=150°，∠DOE=80°，∠AOD+∠BOD=180°， ∴∠BOE=50°， ∴∠AOF=∠BOE=50°， 故答案为：50°.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型：单选题

    下列判断正确的个数是( )

    ①锐角的补角一定是钝角；②一个角的补角一定大于这个角；③锐角和钝角互补；④如果两个角是同一个角的补角，那么它们相等．

    A. 0个 B. 1个 C. 2个 D. 3个

    C 【解析】试题解析：锐角的补角一定是钝角，①正确； 钝角的补角小于这个角，②错误； 锐角和钝角不一定互补，③错误； 如果两个角是同一个角的补角，那么它们相等，④正确； 正确的判断有2个． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.3 多项式与多项式相乘 同步练习 题型：解答题

    已知(x+ay)(x+by)=x2-11xy+6y2,求整式3(a+b)-2ab的值.

    -45 【解析】试题分析：直接利用多项式乘法运算法则计算进而合并同类项得出a+b，ab的值，即可得出答案． 试题解析：【解析】 因为(x+ay)(x+by)=x2+(a+b)xy+aby2=x2-11xy+6y2， 所以a+b=-11，ab=6． 所以3(a+b)-2ab=3×(-11)-2×6=-33-12=-45．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.3 多项式与多项式相乘 同步练习 题型：填空题

    如图,长方形ABCD的面积为________.(用含x的式子表示) 

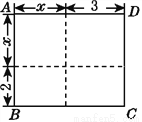
    x2+5x+6 【解析】【解析】 长方形ABCD的面积=（x+2）（x+3）=x2+5x+6．故答案为：x2+5x+6．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.2幂的乘方与积的乘方 第1课时 幂的乘方 同步练习 题型：解答题

    已知x+4y=5,求4x·162y的值.

    1024 【解析】分析：根据积的乘方的逆用，把4x·162y化为4x+4y，代入即可. 本题解析： ∵x+4y=5, ∴4x·162y=4x·44y=4x+4y=45=1 024

    查看答案和解析>>

    科目：初中数学 来源：北师大版 七年级数学下册 第一章　整式的乘除 1.4 整式的乘法 多项式与多项式相乘 同步课时练习题 题型：单选题

    设M＝(x－3)(x－7)，N＝(x－2)(x－8)，则M与N的关系为( )

    A. M＜N B. M＞N

    C. M＝N D. 不能确定

    B 【解析】由于M=（x-3）（x-7）=x2-10x+21，N=（x-2）（x-8）=x2-10x+16，可以通过比较M与N的差得出结果． 【解析】 ∵M=（x-3）（x-7）=x2-10x+21， N=（x-2）（x-8）=x2-10x+16， M-N=（x2-10x+21）-（x2-10x+16）=5， ∴M>N． 故选B． “点睛”本题主要考查多项式乘以多项式的...

    查看答案和解析>>

    同步练习册答案