
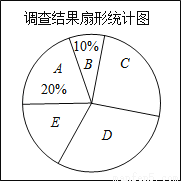
2014年全国两会民生话题成为社会焦点.合肥市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了合肥市部分市民,并对调查结果进行整理.绘制了如图所示的不完整的统计图表.
组别 | 焦点话题 | 频数(人数) |
A | 食品安全 | 80 |
B | 教育医疗 | m |
C | 就业养老 | n |
D | 生态环保 | 120 |
E | 其他 | 60 |
请根据图表中提供的信息解答下列问题:
(1)填空:m= ,n= .扇形统计图中E组所占的百分比为 %;
(2)合肥市人口现有750万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期末测评 题型:填空题
若关于x的分式方程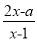 =1的解为正数,那么字母a的取值范围是_______.
=1的解为正数,那么字母a的取值范围是_______.
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型:解答题
某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 | 管理人员 | 普通工作人员 | |||||
人员结构 | 总经理 | 部门经理 | 科研人员 | 销售人员 | 高级技工 | 中级技工 | 勤杂工 |
员工数(名) | 1 | 3 | 2 | 3 | 24 | 1 | |
每人月工资(元) | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数x为2500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资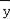 (结果保留整数),并判断
(结果保留整数),并判断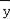 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.

查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型:单选题
下图中①表示的是组合在一起的模块,在②③④⑤四个图形中,是这个模块的俯视图的是( )

A. ② B. ③ C. ④ D. ⑤
A 【解析】②是该几何体的俯视图;③是该几何体的左视图和主视图;④、⑤不是该几何体的三视图. 故选A.查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:解答题
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
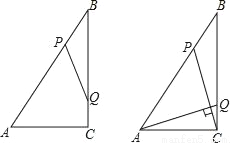
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
(1) t=1或 ;(2) 【解析】试题分析: (1)由∠B是△BPQ与△ABC的公共角,可知,若两三角形相似,存在两种情况:①△BPQ∽△BAC;②△BPQ∽△BCA;分这两种情况结合相似三角形的性质和题意即可解得对应的t的值; (2)如图1,过P作PM⊥BC于点M,AQ,CP交于点N,由题意可知:当AQ⊥CP时,△ACQ∽△CMP,由相似三角形的性质列出比例式即可解得对应的t...查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:填空题
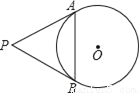
如图,PA、PB是⊙O的切线,切点分别为A、B,已知⊙O的半径为2,∠P=60°,则弦AB的长为_____.
查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学一模试卷 题型:单选题
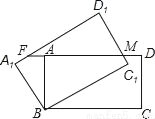
如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=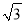 ,则AF的长度为( )
,则AF的长度为( )
A. 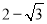 B.
B. 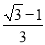 C.
C. 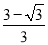 D.
D. 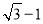
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:填空题
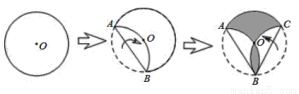
如图,将半径为3的圆形纸片,按下列顺序折叠.若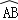 和
和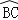 都经过圆心O,则阴影部分的面积是 (结果保留π).
都经过圆心O,则阴影部分的面积是 (结果保留π).
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型:单选题
若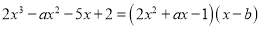 ,则a+b=
,则a+b=
A. -2 B.  C. 2 D. 4
C. 2 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com