
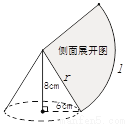
已知圆锥底面半径为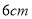 ,高为
,高为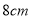 ,则它的侧面展开图的面积为 __________
,则它的侧面展开图的面积为 __________ 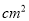 .
.
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源:2018人教版七年级数学下册练习:第八章达标检测卷 题型:填空题
若2x2a-5b+ya-3b=0是二元一次方程,则a=______,b=______.
-2 -1 【解析】根据二元一次方程的定义可得x,y的指数都是1, 由二元一次方程定义得: , 故答案为:a=-2,b=-1.查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
如图,在△ABC中,AB=AC,AH⊥BC,垂足为点H,如果AH=BC,那么sin∠BAC的值是_____.
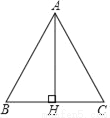
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:解答题
设函数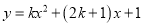 (
(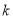 为实数)
为实数)
⑴.写出其中的两个特殊函数,使它们的图象不全是抛物线,并且在同一坐标系中,用描点法画出它们的图像;
⑵.根据所画图像,猜想出:对任意实数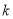 ,函数的图象都具有的特征,并给予证明;
,函数的图象都具有的特征,并给予证明;
⑶.对于任意负实数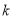 ,当
,当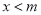 时,
时, 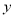 随
随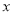 的增大而增大,试求
的增大而增大,试求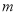 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:解答题
用配方法解方程: 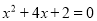
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:单选题
某商场四月份的利润为28万元,预计六月份的利润将达到40万元,设利润每月平均增长率为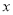 ,那么根据题意所列方程正确的是( )
,那么根据题意所列方程正确的是( )
A. 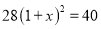 B.
B. 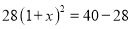 C.
C. 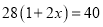 D.
D. 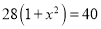
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:单选题
一元二次方程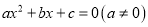 无实数根,则
无实数根,则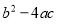 满足的条件是( )
满足的条件是( )
A. 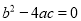 B.
B. 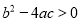 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期九年级期末质量检测数学试卷 题型:单选题
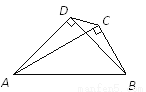
如图,在Rt△ABC和Rt△ABD中,∠ADB=∠ACB=90°,∠BAC=30°,AB=4,AD=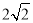 ,连接DC,将Rt△ABC绕点B顺时针旋转一周,则线段DC长的取值范围是
,连接DC,将Rt△ABC绕点B顺时针旋转一周,则线段DC长的取值范围是
A. 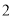 ≤DC≤
≤DC≤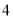 B.
B. 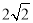 ≤DC≤
≤DC≤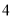
C. 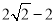 ≤DC≤
≤DC≤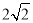 D.
D. 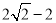 ≤DC≤
≤DC≤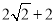
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第九章达标检测卷 题型:填空题
已知x=3是方程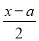 —2=x—1的解,那么不等式(2—
—2=x—1的解,那么不等式(2—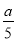 )x<
)x<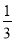 的解集是______.
的解集是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com