
��ͼ��AC��?ABCD�ĶԽ��ߣ���BAC����DAC.
(1)��֤��AB��BC��
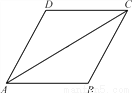
(2)��AB��2��AC��2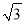 ����?ABCD�������
����?ABCD�������

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���˽̰����꼶�²� ��1-3�� �ۺϲ��Ծ� ���ͣ���ѡ��
һ����ż��������ƽ������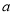 ����ô�������ż�����ڵ���һ����ż��������ƽ�����ǣ�������
����ô�������ż�����ڵ���һ����ż��������ƽ�����ǣ�������
A. 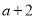 B.
B. 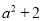 C.
C. 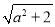 D.
D. 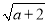
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ2017-2018ѧ��Ⱦ��꼶���ϣ���ѧ��һ���¿��Ծ���11�·ݣ�(������) ���ͣ������
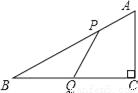
��ͼ���ڡ�ABC�У���C=90�㣬AB=10��BC=8��P��Q�ֱ���AB��BC���ϵĵ㣬��AP=BQ=a ������0��a��8����
��1����PQ��BC����a��ֵ��
��2����PQ=BQ�����߶�CQ���ŵ�Q��ת180�㣬���б��C�Ķ�Ӧ��C���Ƿ������߶�QB�ϣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ2017-2018ѧ��Ⱦ��꼶���ϣ���ѧ��һ���¿��Ծ���11�·ݣ�(������) ���ͣ���ѡ��
�����ABC�ס�A��B��C�䣬BC=3��B��C��=1.8�����A��B��C�����ABC�����Ʊ�Ϊ( )
A.5��3 B.3��2 C.2��3 D.3��5
D �������� ����������������������εĶ�Ӧ�ߵıȵ������Ʊȼ��ɵõ����. �ߡ�ABC�ס�A��B��C�䣬BC=3��B��C��=1.8 ���A��B��C�����ABC�����Ʊ�= B��C���BC=1.8��3=3��5 ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ2017-2018ѧ��Ⱦ��꼶���ϣ���ѧ��һ���¿��Ծ���11�·ݣ�(������) ���ͣ���ѡ��
��ͼ����ABC�У�D��E��BC���ϵĵ㣬BD��DE��EC=3��2��1��M��AC���ϣ�CM��MA=1��2��BM��AD��AE��H��G����BH��HG��GM���ڣ� ��
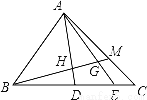
A. 4��2��1 B. 5��3��1 C. 25��12��5 D. 51��24��10
D ������������EM�� ��CE��CD=CM��CA=1��3 ��EMƽ����AD ���BHD�ס�BME����CEM�ס�CDA ��HD��ME=BD��BE=3��5��ME��AD=CM��AC=1��3 ��AH=��3����ME�� ��AH��ME=12��5 ��HG��GM=AH��EM=12��5 ��GM=5k��GH=12k�� ��BH��HM=3��2=BH��17k ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018����꼶�п���ѧר�⸴ϰͬ����ϰ�⣺ƽ���ı��� ���ͣ������
��ͼ������ABCD���ŶԽ���BD�۵���ʹ��C����C�䴦��BC�佻AD�ڵ�E��AD��8��AB��4����DE�ij�Ϊ____________��
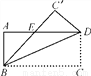
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018����꼶�п���ѧר�⸴ϰͬ����ϰ�⣺ƽ���ı��� ���ͣ���ѡ��
���������У�������ǣ� ��
A. ƽ���ı��εĶԽ�����ƽ��
B. ���εĶԽ����ഹֱƽ��
C. ���εĶԽ�������һ��ഹֱƽ��
D. ��ƽ�����ϵĵ㵽�����ߵľ������
C ���������������������ƽ���ı��ε����ʶ�A�����жϣ��������ε����ʶ�B�����жϣ����ݾ��ε����ʶ�C�����жϣ����ݽ�ƽ���ߵ����ʶ�D�����жϣ� �������� A��ƽ���ı��εĶԽ�����ƽ�֣�����Aѡ���˵����ȷ�� B�����εĶԽ����ഹֱƽ�֣�����Bѡ���˵����ȷ�� C�����εĶԽ�������һ���ƽ�֣�����Cѡ���˵������ D����ƽ�����ϵĵ㵽�����ߵľ�����ȣ�����Dѡ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ���ڡ�ABC�С�ABC=90�㣬��AB=4 cm�� BC=3cm������P��3cm/s���ٶ���A��C�˶�������Qͬʱ��1cm/s���ٶ���B��CB���ӳ��߷����˶�����PQ��AB��D�����˶�ʱ��Ϊ____sʱ����ADP����APΪ���ĵ��������Σ�
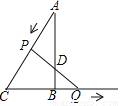
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�ϲ���ѧȫ���ۺϲ��Ծ� ���ͣ������
С���μӡ�Ȥζ��ѧ��ѡ�Σ�������ʦ����һ�����⣬С�����˺�Ϊ�ѣ����ܰ���һ������֪a��b��Ϊ�෴����c��d��Ϊ������|m|=3����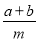 +1+m��cd��ֵΪ���٣�
+1+m��cd��ֵΪ���٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com