
如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
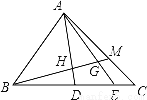
A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
D 【解析】连接EM, ∵CE:CD=CM:CA=1:3 ∴EM平行于AD ∴△BHD∽△BME,△CEM∽△CDA ∴HD:ME=BD:BE=3:5,ME:AD=CM:AC=1:3 ∴AH=(3﹣)ME, ∴AH:ME=12:5 ∴HG:GM=AH:EM=12:5 设GM=5k,GH=12k, ∵BH:HM=3:2=BH:17k ... 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源:人教版七年级下册 第1-3章 综合测试卷 题型:单选题
下列图形中,能由∠1+∠2=180°得到AB∥CD的是( )
A. 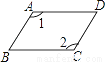 B.
B. 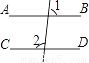
C. 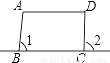 D.
D. 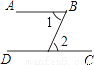
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第2课时) 题型:解答题
在某一电路中,保持电压不变,电流 I(安培)和电阻 R(欧姆)成反比例,当电阻 R=5欧姆时,电流 I=2安培.
(1)求 I与 R之间的函数关系式;
(2)当电流 I=0.5时,求电阻 R的值;
(3)若电阻的最大值为欧姆20,请你写出电流的范围.
(1) I= ;(2) R=20;(3)电流的范围是大于等于0.5安培. 【解析】试题分析: (1)由题意可设,代入 R=5,I=2即可求得的值,从而可得I与 R之间的函数关系式; (2)将I=0.5代入(1)中所得函数关系式即可求得对应的R的值; (3)将电阻R最大=20代入(1)中所得函数关系式即可求得对应的的电流I的最小值,由此即可电流I的取值范围. 试题解析:...查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:填空题
如图所示,Rt△AOB中,∠AOB=90°,OA=4,OB=2,点B在反比例函数y= 图象上,则图中过点A的双曲线解析式是_____.
图象上,则图中过点A的双曲线解析式是_____.
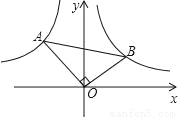
查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:单选题
如图所示是两根标志杆在地面上的影子,根据这些地面上的投影,你能判断出在灯光下的影子的是( )
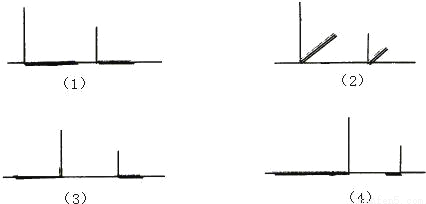
A. (1)和(2) B. (2)和(3) C. (2)和(4) D. (3)和(4)
D 【解析】根据物体的顶端和影子顶端的连线必经过光源可得图中连接物的顶端与影子的顶端的两条直线应有交点,故只有(3)(4)符合题意,故选D.查看答案和解析>>
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:解答题
如图,AC是?ABCD的对角线,∠BAC=∠DAC.
(1)求证:AB=BC;
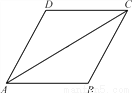
(2)若AB=2,AC=2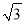 ,求?ABCD的面积.
,求?ABCD的面积.
查看答案和解析>>
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:填空题
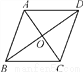
如图,在菱形ABCD中,AC,BD相交于点O,若∠BCO=55°,则∠ADO=____________.
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
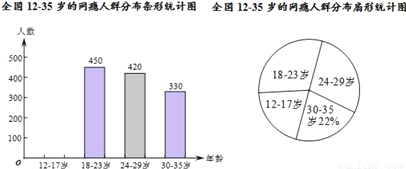
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
(1)a=300;(2)108°;(3)12~23岁的人数为400万 【解析】试题分析:(1)根据30-35岁的人数和所占的百分比求调查的人数; (2)从调查的总人数中减去已知的三组的人数,即可得到12-17岁的人数,据此补全条形统计图; (3)先计算18-23岁的人数占调查总人数的百分比,再计算这一组所对应的圆心角的度数; (4)先计算调查中12﹣23岁的人数所占的百分比...查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学 第三章 图形的平移与旋转 单元检测卷 题型:单选题
如图,不是平移设计的是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com