
y=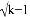 x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0根的情况为( )
x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0根的情况为( )
A. 没有实数根 B. 有一个实数根
C. 有两个不相等的实数根 D. 有两个相等的实数根
A 【解析】∵y=x+1是关于x的一次函数, , . ∴方程没有实数根; 故选A.科目:初中数学 来源:江苏省2018届九年级12月月考数学试卷 题型:解答题
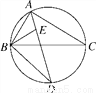
如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
查看答案和解析>>
科目:初中数学 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:填空题
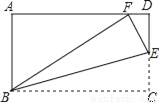
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为_____.
【答案】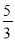
【解析】试题分析:由矩形的性质可得AB=CD=4,AD=BC=5,再根据折叠的性质可得CE=EF,BF=BC=5.在Rt△ABF中,根据勾股定理可求得AF=4,设CE=x,在Rt△EDF中,由勾股定理可得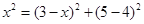 ,解得x=
,解得x=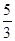 ,即CE的长为
,即CE的长为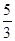 .
.
考点:矩形的性质;折叠的性质;勾股定理.
【题型】填空题
【结束】
14
观察下列各式: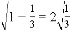 ,
,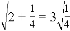 ,
,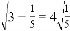 …请你将发现的规律用含自然数n(n≥1)的代数式表达来_____________。
…请你将发现的规律用含自然数n(n≥1)的代数式表达来_____________。
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:解答题
已知关于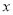 的一元二次方程
的一元二次方程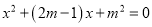 有两个实数根
有两个实数根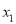 和
和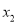 .
.
(1)求实数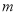 的取值范围;
的取值范围;
(2)当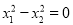 时,求
时,求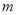 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:填空题
关于x的一元二次方程x2-3x+m=0有实数根α、β,且α2+β2=17,则m的值是______.
-4 【解析】一元二次方程x2-3x+m=0有实数根,可得△=b2-4ac=9-4m≥0,解得m≤.根据根与系数的可得 ,所以α2+β2=,解得m=-4.查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:单选题
已知α、β是方程2x2﹣3x﹣1=0的两个实数根,则(α﹣2)(β﹣2)的值是( )
A.  B.
B. 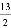 C. 3 D.
C. 3 D. 
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:解答题
解方程:x2+2x﹣3=0.(因式分解法)
x1=1,x2=﹣3. 【解析】x2+2x﹣3=0, (x-1)(x+3)=0, x1=1,x2=-3.查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:解答题
解方程:x(x﹣1)=4(1﹣x).(因式分解法)
x1=1,x2=﹣4. 【解析】x(x﹣1)+4(x﹣1)=0, (x﹣1)(x+4)=0, 所以x1=1,x2=﹣4.查看答案和解析>>
科目:初中数学 来源:江苏省句容市片区合作共同体2017-2018学年年八年级上学期第二次学情测试数学试卷 题型:填空题
若等腰三角形的两边长分别为4和8,则这个三角形的周长为 .
C 【解析】试题分析:若腰为,则不能组成三角形,舍;若腰为,则能组成三角形,且周长为.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com