
如图,四边形ABCD为一个矩形纸片,AB=3,BC=2,动点P自D点出发沿DC方向运动至C点后停止,△ADP以直线AP为轴翻折,点D落在点D1的位置,设DP=x,△AD1P与原纸片重叠部分的面积为y.
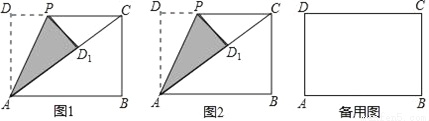
(1)当x为何值时,直线AD1过点C?
(2)当x为何值时,直线AD1过BC的中点E?
(3)求出y与x的函数表达式.
(1);(2);(3) 【解析】试题分析:(1)根据折叠得出AD=AD1=2,PD=PD1=x,∠D=∠AD1P=90°,在Rt△ABC中,根据勾股定理求出AC,在Rt△PCD1中,根据勾股定理得出方程,求出即可; (2)连接PE,求出BE=CE=1,在Rt△ABE中,根据勾股定理求出AE,求出AD1=AD=2,PD=PD1=x,D1E=﹣2,PC=3﹣x,在Rt△PD1E和Rt△PC... 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:填空题
轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3h,若船在静水中速度为26km/h,水流速度为2km/h,则A港和B港相距_____km.
504 【解析】试题分析:设轮船从A港顺流行驶到B港所需的时间为t,则从B港逆流返回A港的时间为t+3,因船速为26千米/小时,水速为2千米/时,则顺流速度为26+2=28km/h,逆流速度为26-2=24km/h,则有28t=24(t+3),解得t=18,所以A港和B港的距离为28×18=504km.查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:解答题
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点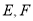 分别在正方形
分别在正方形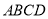 的边
的边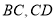 上,
上, 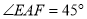 ,连接
,连接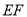 ,则
,则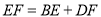 ,试说明理由.
,试说明理由.
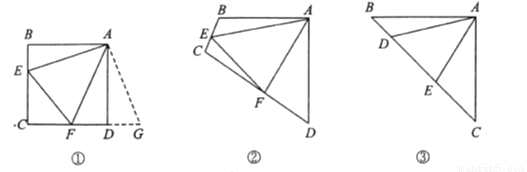
(1)思路梳理
因为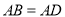 ,所以把
,所以把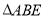 绕点
绕点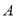 逆时针旋转90°至
逆时针旋转90°至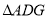 ,可使
,可使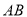 与
与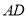 重合.因为
重合.因为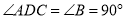 ,所以
,所以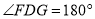 ,点
,点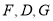 共线.
共线.
根据 ,易证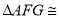 ,得
,得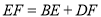 .请证明.
.请证明.
(2)类比引申
如图②,四边形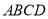 中,
中, 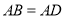 ,
, 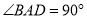 ,点
,点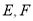 分别在边
分别在边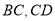 上,
上, 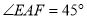 .若
.若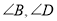 都不是直角,则当
都不是直角,则当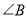 与
与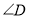 满足等量关系时,
满足等量关系时, 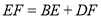 仍然成立,请证明.
仍然成立,请证明.
(3)联想拓展
如图③,在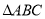 中,
中, 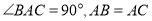 ,点
,点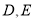 均在边
均在边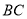 上,且
上,且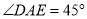 .猜想
.猜想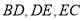 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:填空题
如果等腰三角形的底角是50°,那么这个三角形的顶角的度数是___________
80° 【解析】试题解析:180°-50°×2 =180°-100° =80°. 故这个三角形的顶角的度数是80°.查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:单选题
在△ABC中,∠A=70°,∠B=55°,则△ABC是( )
A. 钝角三角形 B. 等腰三角形
C. 等边三角形 D. 等腰直角三角形
B 【解析】【解析】 ∵在△ABC中,∠A=70°,∠B=55°,∴∠C=180°﹣∠A﹣∠B=55°,∴∠B=∠C,∴△ABC是等腰三角形.故选B.查看答案和解析>>
科目:初中数学 来源:山东省济南市2018届九年级1月月考数学试卷 题型:填空题
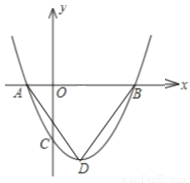
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D, 其图象与x轴的交点A、B的横坐标分别为﹣1,3.与y轴负半轴交于点C,当a=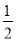 时,△ABD是_______三角形;要使△ACB为等腰三角形,则a值为______
时,△ABD是_______三角形;要使△ACB为等腰三角形,则a值为______
查看答案和解析>>
科目:初中数学 来源:山东省济南市2018届九年级1月月考数学试卷 题型:单选题
.二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正确结论的个数是( )
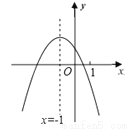
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】【解析】 ∵抛物线和x轴有两个交点,∴b2﹣4ac>0,∴4ac﹣b2<0,∴①正确; ∵对称轴是直线x=﹣1,和x轴的一个交点在点(0,0)和点(1,0)之间,∴抛物线和x轴的另一个交点在(﹣3,0)和(﹣2,0)之间,∴把(﹣2,0)代入抛物线得:y=4a﹣2b+c>0,∴4a+c>2b,∴②错误; ∵把x=1代入抛物线得:y=a+b+c<0,∴2a+2b+2c...查看答案和解析>>
科目:初中数学 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:解答题
某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,
(1)每轮感染中平均一台电脑会感染几台电脑?
(2)若该病毒得不到有效控制,第3轮感染后,被感染的电脑会不会超过700台?说明理由
8台;会超过700台. 【解析】试题分析:(1)设每轮感染中平均一台电脑会感染台电脑,根据题意列出方程,求出方程的解即可; (2)求出3轮感染后被感染的电脑台数,再比较大小即可. 试题解析:(1)设每轮感染中平均一台电脑会感染台电脑,则依题意得: 整理得: 解得: (不合题意,舍)∴; (2)3轮感染后,被感染的电脑有查看答案和解析>>
科目:初中数学 来源:四川省绵阳市三台县2018届九年级(上)第一学月数学试卷 题型:单选题
方程(x﹣3)2=(x﹣3)的根为( )
A. 3 B. 4 C. 4或3 D. ﹣4或3
C 【解析】试题分析:由,移项得: ,提公因式得: , ∴, .故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com