
在△ABC中,∠A=70°,∠B=55°,则△ABC是( )
A. 钝角三角形 B. 等腰三角形
C. 等边三角形 D. 等腰直角三角形
B 【解析】【解析】 ∵在△ABC中,∠A=70°,∠B=55°,∴∠C=180°﹣∠A﹣∠B=55°,∴∠B=∠C,∴△ABC是等腰三角形.故选B. 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:解答题
先化简再求值:2(x3﹣2y2)﹣(x﹣2y)﹣(x﹣3y2+2x3),其中x=﹣3,y=﹣2.
﹣y2﹣2x+2y,-2 【解析】试题分析:先去括号,然后合并同类项,最后代入数值进行计算即可. 试题解析:2(x3﹣2y2)﹣(x﹣2y)﹣(x﹣3y2+2x3)=2x3﹣4y2﹣x+2y﹣x+3y2﹣2x3=﹣y2﹣2x+2y, 当x=﹣3,y=﹣2时,原式=﹣(﹣2)2﹣2×(﹣3)+2×(﹣2)=﹣4+6﹣4=﹣2.查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:单选题
用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象(如图所示),则所解的二元一次方程组是( )
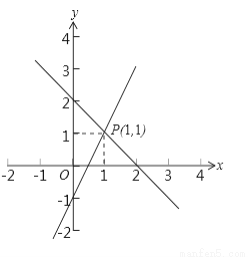
A. 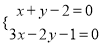 B.
B. 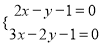 C.
C. 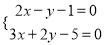 D.
D. 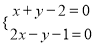
查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:填空题
甲、乙两人同时从同一地点出发,甲往北偏东60°的方向走了12 km,乙往南偏东30°的向走了5 km,这时甲、乙两人相距___________km
13 【解析】试题解析:如图所示, ∵甲往北偏东60°的方向走了12km,乙往南偏东30°的向走了5km, ∴∠AOB=90°, ∴AB==13(km).查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:单选题
下列说法中正确的是( )
A. 两个直角三角形全等 B. 两个等腰三角形全等
C. 两个等边三角形全等 D. 两条直角边对应相等的直角三角形全等
D 【解析】试题解析:A、两个直角三角形只能说明有一个直角相等,其他条件不明确,所以不一定全等,故本选项错误; B、两个等腰三角形,腰不一定相等,夹角也不一定相等,所以不一定全等,故本选项错误; C、两个等边三角形,边长不一定相等,所以不一定全等,故本选项错误; D、它们的夹角是直角相等,可以根据边角边定理判定全等,正确. 故选D.查看答案和解析>>
科目:初中数学 来源:山东省济南市2018届九年级1月月考数学试卷 题型:解答题
如图,四边形ABCD为一个矩形纸片,AB=3,BC=2,动点P自D点出发沿DC方向运动至C点后停止,△ADP以直线AP为轴翻折,点D落在点D1的位置,设DP=x,△AD1P与原纸片重叠部分的面积为y.
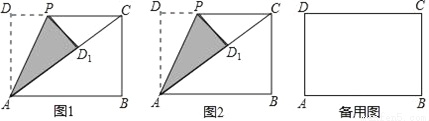
(1)当x为何值时,直线AD1过点C?
(2)当x为何值时,直线AD1过BC的中点E?
(3)求出y与x的函数表达式.
(1);(2);(3) 【解析】试题分析:(1)根据折叠得出AD=AD1=2,PD=PD1=x,∠D=∠AD1P=90°,在Rt△ABC中,根据勾股定理求出AC,在Rt△PCD1中,根据勾股定理得出方程,求出即可; (2)连接PE,求出BE=CE=1,在Rt△ABE中,根据勾股定理求出AE,求出AD1=AD=2,PD=PD1=x,D1E=﹣2,PC=3﹣x,在Rt△PD1E和Rt△PC...查看答案和解析>>
科目:初中数学 来源:山东省济南市2018届九年级1月月考数学试卷 题型:填空题
如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于_______海里.
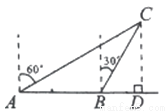
查看答案和解析>>
科目:初中数学 来源:福建省汀东教研片六校2018届九年级10月月考数学试卷 题型:解答题
某商场以每件42元的价钱购进一种服装,根据试销得知:这种服装每天的销售量t(件),与每件的销售价x(元/件)可看成是一次函数关系:t=-3x+204.
(1)写出商场卖这种服装每天的销售利润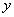 与每件的销售价
与每件的销售价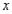 之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
(2)通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适;最大销售利润为多少?
当每件的销售价为55元时,可取得最大利润,每天最大销售利润为507元. 【解析】试题分析:(1)商场的利润是由每件商品的利润乘每天的销售的数量所决定.在这个问题中,每件服装的利润为(x-42),而销售的件数是(-3x+204),由销售利润y=(售价-成本)×销售量,那么就能得到一个y与x之间的函数关系,这个函数是二次函数. (2)要求销售的最大利润,就是要求这个二次函数的最大值. ...查看答案和解析>>
科目:初中数学 来源:四川省绵阳市三台县2018届九年级(上)第一学月数学试卷 题型:单选题
函数y=ax+b和y=ax2+bx+c在同一直角坐标系内的图象大致是( )
A. 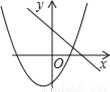 B.
B. 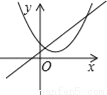 C.
C. 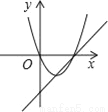 D.
D. 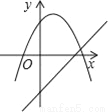
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com