
已知抛物线经过点(0,4),(1,﹣1),(2,4),那么它的对称轴是直线( )
A. x=﹣1 B. x=1 C. x=3 D. x=﹣3
B 【解析】试题分析:由二次函数图象的对称性即可求出对称轴. 【解析】 ∵点(0,4)与(2,4)关于抛物线对称, ∴对称轴为x=1. 故选B. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(2)测试 题型:单选题
△ABC绕着A点旋转后得到△AB′C′,若∠BAC′=130°,∠BAC=80°,则旋转角等于( )
A. 50° B. 210° C. 50°或210° D. 130°
C 【解析】因为∠BAC′=130°,∠BAC=80°, 所以如图1, ∠CAC′=∠BAC’ -∠BAC=50°, 如图2, ∠CAC′=∠BAC’ +∠BAC=210°, 所以旋转角等于50°, 210°,故选C.查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试4 题型:单选题
在元旦游园晚会上有一个闯关活动:将5张分别画有等腰梯形、圆、平行四边形、等腰三角形、菱形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张,如果翻开的图形是轴对称图形,就可以过关.那么一次过关的概率是( )
A. 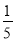 B.
B. 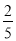 C.
C. 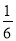 D.
D. 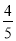
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:填空题
二次函数y=x2-2x-3的图象关于原点O(0,0)对称的图象的解析式是_________.
Y=_-x2-2x+3(写成顶点式也对) 【解析】利用抛物线的性质. 【解析】 可先从抛物线y=x2-2x-3上找三个点(0,-3),(1,-4),(-1,0).它们关于原点对称的点是(0,3),(-1,4),(1,0).可设新函数的解析式为y=ax2+bx+c,则c=3,a-b+c=4,a+b+c=0.解得a=-1,b=-2,c=3.故所求解析式为:y=-x2-2x+3. ...查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:单选题
抛物线的图象如图所示,根据图象可知,抛物线的解析式可能是( )
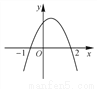
A. y=x2-x-2 B. y=-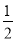 x2-
x2-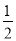 x+2 C. y=-
x+2 C. y=-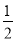 x2-
x2-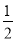 x+1 D. y=-x2+x+2
x+1 D. y=-x2+x+2
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.
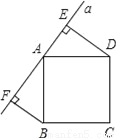
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
△ABC和△FED中,BE=FC,∠A=∠D.当添加条件_________时(只需填写一个你认为正确的条件),就可得到△ABC≌△DFE,依据是________.
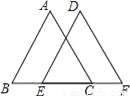
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
如图,AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
(1)若以“SAS”为依据,需添加条件____________;
(2)若以“HL”为依据,需添加条件_____________.
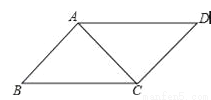
查看答案和解析>>
科目:初中数学 来源:北师大版(2012) 九年级上册同步练习:1.2矩形的性质 题型:解答题
如图所示,在矩形ABCD中,四个内角平分线相交于E、F, 若AB= 8cm,Ad=20cm,求EF的长度.
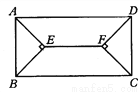
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com