
二次函数y=x2-2x-3的图象关于原点O(0,0)对称的图象的解析式是_________.
Y=_-x2-2x+3(写成顶点式也对) 【解析】利用抛物线的性质. 【解析】 可先从抛物线y=x2-2x-3上找三个点(0,-3),(1,-4),(-1,0).它们关于原点对称的点是(0,3),(-1,4),(1,0).可设新函数的解析式为y=ax2+bx+c,则c=3,a-b+c=4,a+b+c=0.解得a=-1,b=-2,c=3.故所求解析式为:y=-x2-2x+3. ...科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(2)测试 题型:解答题
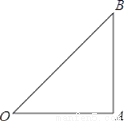
如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(1)请你画出将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1;
(2)线段OA1的长度是______,∠AOB1的度数是______;
(3)连接AA1,求证:四边形OAA1B1是平行四边形.
查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试4 题型:解答题
将下面事件的字母写在最能代表它的概率的点上.
A.投掷一枚硬币时,得到一个正面.
B.在一小时内,你步行可以走80千米.
C.给你一个骰子中,你掷出一个3.
D.明天太阳会升起来.
查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试4 题型:单选题
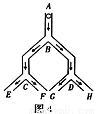
如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达 H 点的概率是( )
A. 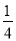 B.
B. 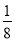 C.
C. 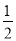 D.
D. 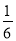
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:解答题
已知二次函数的图象如图所示,求此抛物线的解析式.
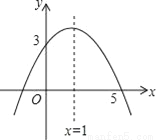
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:填空题
若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为__________________.
y = 【解析】试题分析:设抛物线的解析式为y=a(x-2)2+1,将点B(1,0)代入解析式即可求出a的值,从而得到二次函数解析式. 试题解析:设抛物线的解析式为y=a(x-2)2+1, 将B(1,0)代入y=a(x-2)2+1得, a=-1, 函数解析式为y=-(x-2)2+1, 展开得y=-x2+4x-3.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:单选题
已知抛物线经过点(0,4),(1,﹣1),(2,4),那么它的对称轴是直线( )
A. x=﹣1 B. x=1 C. x=3 D. x=﹣3
B 【解析】试题分析:由二次函数图象的对称性即可求出对称轴. 【解析】 ∵点(0,4)与(2,4)关于抛物线对称, ∴对称轴为x=1. 故选B.查看答案和解析>>
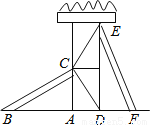
科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=___________度.
查看答案和解析>>
科目:初中数学 来源:重庆市华东师大版2016-2017学年七年级下学期期中考试数学试卷 题型:单选题
当x=1时,ax+b+1的值为-2,则(a+b-1)(1-a-b)的值为( )
A. -16 B. -8 C. 8 D. 16
A 【解析】试题解析:当时, 的值为 即: 故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com