
如果x2+x﹣1=0,则代数式x3+2x2﹣7的值为_____.
-6 【解析】【解析】 ∵x2+x﹣1=0,∴x2+x=1,∴x3+2x2﹣7=x3+x2+x2﹣7=x(x2+x)+x2﹣7=x+x2﹣7=﹣6. 故答案为:﹣6.科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(三) 题型:单选题
在△ABC中,∠A=120°,AB=4,AC=2,则sinB的值是( )
A. 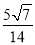 B.
B. 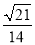 C.
C. 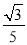 D.
D. 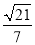
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:填空题
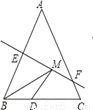
如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____________
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
以下图标是轴对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:解答题
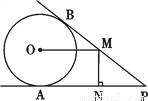
如图,PA,PB分别与⊙O相切于点A,B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM = AN;
(2)若⊙O的半径R = 3,PA = 9,求OM的长.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:填空题
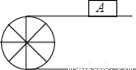
如图半径为30cm的转动轮转过80°时,传送带上的物体A平移的距离为_____.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:单选题
如图,圆锥的底面半径OB=6cm,高OC=8cm.则这个圆锥的侧面积是( )
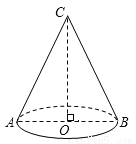
A. 30cm2 B. 30πcm2 C. 60πcm2 D. 120cm2
C 【解析】试题分析:先利用勾股定理计算出圆锥的母线长=,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式计算这个圆锥漏斗的侧面积=•2π•6•10=60π(cm2). 故选C.查看答案和解析>>
科目:初中数学 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:填空题
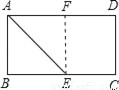
如图所示,一张矩形纸片,要折叠出一个最大的正方形,小明把矩形上的一个角沿折痕AE翻折上去,使AB与AD边上的AF重合,则四边形ABEF就是一个大的正方形,他判定的方法是_____.
查看答案和解析>>
科目:初中数学 来源:江西省2017年秋人教七年级数学上册期末模拟卷 题型:单选题
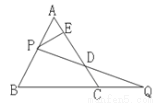
如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为 ( )
A.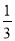 B.
B.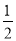 C.
C.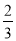 D.不能确定
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com