
如图,不能判断l1∥l2的条件是( )

A. ∠1=∠3 B. ∠2+∠4=180° C. ∠4=∠5 D. ∠2=∠3
D 【解析】A. ∠1=∠3正确,内错角相等两直线平行; B. ∠2+∠4=180°正确,同旁内角互补两直线平行; C. ∠4=∠5正确,同位角相等两直线平行; D. ∠2=∠3错误,它们不是同位角、内错角、同旁内角,故不能推断两直线平行。 故选D.科目:初中数学 来源:2018年1月北京市海淀区初三上数学期末试卷 题型:单选题
在△ABC中,∠C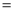 90°.若AB
90°.若AB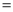 3,BC
3,BC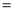 1,则
1,则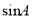 的值为( )
的值为( )
A. 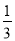 B.
B. 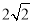 C.
C. 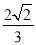 D.
D. 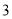
查看答案和解析>>
科目:初中数学 来源:云南省2016-2017学年八年级上学期期末考试数学试卷 题型:单选题
某农场挖一条480米的渠道,开工后,每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖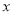 米,那么下列方程正确的是( )
米,那么下列方程正确的是( )
A.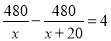
B.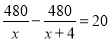
C.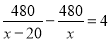
D.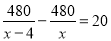
查看答案和解析>>
科目:初中数学 来源:2016-2017学年第二学期无锡市惠山区初一数学期末试卷 题型:填空题
如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=88°,则∠C的度数为=___________.

查看答案和解析>>
科目:初中数学 来源:2016-2017学年第二学期无锡市惠山区初一数学期末试卷 题型:单选题
设△ABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……, 依此类推,则S5的值为( )
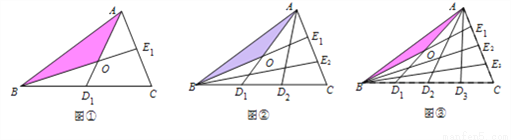
A.  B.
B.  C.
C. 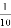 D.
D. 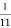
查看答案和解析>>
科目:初中数学 来源:黑龙江省安达市2017-2018学年七年级上学期期末质量检测数学试卷 题型:解答题
有n个数,第一个记为a1,第二个.记为a2;……,第n个记为ax,若 a1= ,且从第二个数起,每个数都等于“1与它前面那个数的差的倒数”
,且从第二个数起,每个数都等于“1与它前面那个数的差的倒数”
(1)则a2=______;a3 =______;a4 =______.
(2)根据(1)的计算结果,猜想a2005=______;a2006=______.
(3)计算:  的值.
的值.
查看答案和解析>>
科目:初中数学 来源:黑龙江省安达市2017-2018学年七年级上学期期末质量检测数学试卷 题型:解答题
12﹣(﹣18)+(﹣7)﹣15;
8 【解析】试题分析:有理数的加减混合运算,一般应统一成加法运算,再运用运算律进行简化计算. 试题解析:原式=12+18?7?15=30?22=8.查看答案和解析>>
科目:初中数学 来源:2017学年嘉定区第一学期九年级期终学业质量调研测试(2018年初三一模) 题型:解答题
在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC= ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索:  的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源:山西大学附中2018届九年级10月月考数学试卷 题型:单选题
下列命题是真命题的是( )
A. 四边都是相等的四边形是矩形 B. 菱形的对角线相等
C. 对角线互相垂直的平行四边形是正方形 D. 对角线相等的平行四边形是矩形
D 【解析】试题分析:选项A,四边都相等的四边形是菱形,选项A是假命题;选项B,矩形的对角线相等,选项B是假命题;选项C,对角线互相垂直平分且相等的平行四边形是正方形,选项C是假命题;选项D,对角线相等的平行四边形是矩形,选项D是真命题,故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com