练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，四边形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为 ．

    100° 【解析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值。作DA延长线AH, ∵∠DAB=120°， ∴∠HAA′=60°， ∴∠AA′M+∠A″=∠HAA′=60°， ∵∠MA′A=∠MAA′，∠NAD=∠A″， 且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM， ∴∠...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：贵州铜仁伟才学校2017-2018学年八年级上学期期中考试数学试卷 题型：填空题

    计算： =_____．

    -1 【解析】 = = =-1

    查看答案和解析>>

    科目：初中数学 来源：江西婺源县2016-2017学年第一学期期末考试七年级数学试卷 题型：解答题

    甲路工艺伞由甲、乙两部件各一个组成，甲路工艺伞厂每天能制作甲部件400个，或者制作乙部件200个，现要在30天内制作最多的该种工艺伞，则甲、乙两种部件各应制作多少天？

    甲部件应制作10天，则乙部件应制作20天． 【解析】试题分析：利用配套关系，列方程，求解. 试题解析： 设甲部件应制作x天，则乙部件应制作（30﹣x）天， 由题意得：400x=200（30﹣x）， 解得： x=10， 所以，乙部件应制作30﹣x=30﹣10=20（天）， 答：甲部件应制作10天，则乙部件应制作20天．

    查看答案和解析>>

    科目：初中数学 来源：江西婺源县2016-2017学年第一学期期末考试七年级数学试卷 题型：单选题

    若a + b = 6，则18－2a－2b =（ ）

    A. 6 B. －6 C. －24 D. 12

    A 【解析】18－2a－2b =18-2(a+b)=18-2=6.故选A.

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市鄞州区九校2017-2018学年八年级上册数学第一次月考试卷 题型：解答题

    如图：已知等边△ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DM⊥BC，垂足为M．

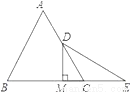
    （1）求∠E的度数．

    （2）求证：M是BE的中点．

    （1）30°；（2）证明见解析. 【解析】试题分析：（1）由等边△ABC的性质可得：∠ACB=∠ABC=60°，然后根据等边对等角可得：∠E=∠CDE，最后根据外角的性质可求∠E的度数； （2）连接BD，由等边三角形的三线合一的性质可得：∠DBC=∠ABC=×60°=30°，结合（1）的结论可得：∠DBC=∠E，然后根据等角对等边，可得：DB=DE，最后根据等腰三角形的三线合一的性质可...

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市鄞州区九校2017-2018学年八年级上册数学第一次月考试卷 题型：填空题

    能将三角形面积平分的是三角形的_______（填中线或角平分线或高线）

    中线 【解析】根据等底等高可得，能将三角形面积平分成相等两部分的是三角形的中线。 故答案为：中线.

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市鄞州区九校2017-2018学年八年级上册数学第一次月考试卷 题型：单选题

    已知△ABC的三个内角三条边长如图所示，则甲、乙、丙三个三角形中,和△ABC全等的图形是（   ）

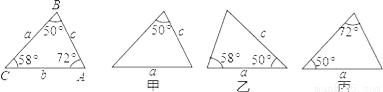
    A. 甲和乙 B. 乙和丙 C. 只有乙 D. 只有丙

    B 【解析】乙和△ABC全等；理由如下： 在△ABC和图乙的三角形中，满足三角形全等的判定方法：SAS， ∴乙和△ABC全等； 在△ABC和图丙的三角形中，满足三角形全等的判定方法：AAS， ∴丙和△ABC全等； 甲与△ABC不全等； 故选：B.

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年河北省张家口市桥东区七年级（下）期末数学试卷 题型：单选题

    如图，△ABC中∠A=30°，E是AC边上的点，先将△ABE沿着BE翻折，翻折后△ABE的AB边交AC于点D，又将△BCD沿着BD翻折，C点恰好落在BE上，此时∠CDB=82°，则原三角形的∠B=（　　）度．

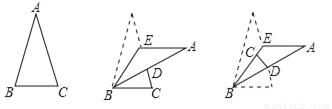
    A. 78° B. 52° C. 68° D. 75°

    A 【解析】在△ABC中，∠A=30°，则∠B+∠C=150°①； 根据折叠的性质知：∠B=3∠CBD，∠BCD=∠C； 在△CBD中，则有：∠CBD+∠BCD=180°﹣82°，即： ∠B+∠C=98°②； ①﹣②，得： ∠B=52°， 解得∠B=78°， 故选A．

    查看答案和解析>>

    科目：初中数学 来源：湖北省黄冈市2017-2018学年八年级（上）期中数学试 题型：解答题

    如图，将△ABC折叠，使点C落在点C′处，折痕为EF．

    （1）若∠1=40°，∠2=20°，求∠C；

    （2）探究∠1，∠2与∠C之间的数量关系．

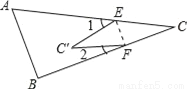
    见解析 【解析】试题分析：（1）根据平角求出和 再根据翻折的性质求出和，然后利用三角形的内角和定理列式进行计算即可得解； （2）用表示出和再根据翻折的性质表示出和，然后根据三角形的内角和定理列式整理即可得解． 试题解析：（1） 由翻折的性质， 在中， （2） 由由翻折的性质， 在中， 所以，

    查看答案和解析>>

    同步练习册答案