练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    的结果是_____________.

    ； 【解析】原式 = = = 故填: .
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省2017-2018学年八年级上学期期中考试数学试卷 题型：单选题

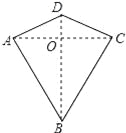
    两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AD=CD，AB=CB，在探究筝形的性质时，得到如下结论：①△ABD≌△CBD；②AC⊥BD；③四边形ABCD的面积=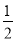AC•BD，其中正确的结论有（ ）

    A. 0个 B. 1个 C. 2个 D. 3个

    D 【解析】试题分析：在△ABD与△CBD中， ，可得△ABD≌△CBD（SSS），故①正确； 根据全等三角形的性质，可得∠ADB=∠CDB，在△AOD与△COD中， ，可得△AOD≌△COD（SAS），可得∠AOD=∠COD=90°，AO=OC，根据垂直的定义可得AC⊥DB，故②正确； 四边形ABCD的面积= =ACBD，故③正确； 故选D．

    查看答案和解析>>

    科目：初中数学 来源：湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷（含答案） 题型：填空题

    如图，有一个长为50cm，宽为30cm，高为40cm的长方体木箱，一根长70cm的木棍________放入（填“能”或“不能”）．

    能 【解析】根据勾股定理可计算出长方体最大容纳长度=,故答案为:能.

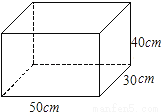
    查看答案和解析>>

    科目：初中数学 来源：河北省2017-2018学年八年级（上）期末复习测试数学试卷 题型：解答题

    已知△ABN和△ACM位置如图所示，AB=AC，∠1=∠2，∠M=∠N．求证：AD=AE．

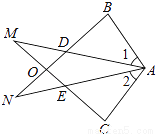
    证明见解析 【解析】试题分析：先证明∠BDA=∠CEA，由SAS证明△ABD≌△ACE，得出对应边相等即可． 试题解析：∵∠M=∠N， ∴∠MDO=∠NEO， ∴∠BDA=∠CEA， ∴在△ABD和△ACE中， ∵ ， ∴△ABD≌△ACE（AAS）， ∴AD=AE．

    查看答案和解析>>

    科目：初中数学 来源：河北省2017-2018学年八年级（上）期末复习测试数学试卷 题型：填空题

    分式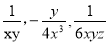的最简公分母是________

    12x3yz 【解析】根据分式的分母分别是：xy，4x3，6xyz，由最简公分母确定方法：从系数（取最小公倍数），字母（所有字母），指数（各字母的最高次幂），可得它们的最简公分母为12x3yz. 故答案为：12x3yz.

    查看答案和解析>>

    科目：初中数学 来源：河北省2017-2018学年八年级（上）期末复习测试数学试卷 题型：单选题

    已知实数a、b满足：ab=1且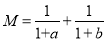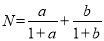， ，则M、N的关系为（　　）

    A. M＞N B. M＜N C. M=N    D. M、N的大小不能确定

    C 【解析】先通分，再利用作差法可由= ， =，因此可得M﹣N=﹣==，由ab=1，可得2﹣2ab=0，即M﹣N=0，即M=N． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：解答题

    如图，二次函数y=x2+2x+c的图象与x轴交于点A和点B（1，0），以AB为边在x轴上方作正方形ABCD，动点P从点A出发，以每秒2个单位长度的速度沿x轴的正方向匀速运动，同时动点Q从点C出发，以每秒1个单位长度的速度沿CB匀速运动，当点Q到达终点B时，点P停止运动，设运动时间为t秒．连接DP，过点P作DP的垂线与y轴交于点E．

    （1）求二次函数的解析式及点A的坐标；

    （2）当点P在线段AO（点P不与A、O重合）上运动至何处时，线段OE的长有最大值，并求出这个最大值；

    （3）在P，Q运动过程中，求当△DPE与以D，C，Q为顶点的三角形相似时t的值；

    （4）是否存在t，使△DCQ沿DQ翻折得到△DC′Q，点C′恰好落在抛物线的对称轴上？若存在，请求出t的值；若不存在，请说明理由．

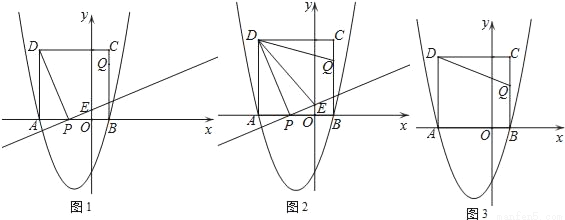
    （1）y=x2+2x﹣3，点A的坐标为（﹣3，0）； （2）点P位于AO的中点时，线段OE的长有最大值； （3）t=1或3或， （4）存在t=． 【解析】试题分析：(1)先将点B的坐标代入解析式求得c的值确定二次函数解析式,令y=0即可求得A点坐标. (2)由DP⊥PE证得△DAP∽△POE,用比例式表示出y与t的关系,根据函数图象的性质可求得OE的最大值. ...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：单选题

    把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜边AB=6，DC=7，把三角板DCE绕点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与CD1交于点O，则线段AD1的长为（　　）

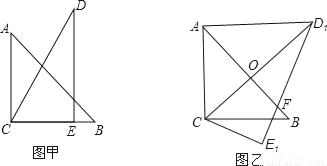
    A. 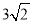B. 5 C. 4 D.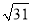

    B 【解析】由旋转的性质可知，在图乙中，∠BCE1=15°，∠D1CE1=60°，AB=6，CD1=CD=7， ∴∠D1CB=60°-15°=45°， 又∵∠ACB=90°， ∴CO平分∠ACB， 又∵AC=BC， ∴CO⊥AB，且CO=AO=BO=AB=3， ∴D1O=CD1-CO=7-3=4，∠AOD1=90°， ∴在Rt△AOD1中，AD1=....

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省苏州市中考数学模拟试卷（三） 题型：解答题

    先化简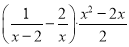，再从0，1，2中选一个合适的x的值代入求值．

    . 【解析】试题分析：原式括号中两项通分并利用同分母分式的减法法则计算，约分得到最简结果，把x=1代入计算即可求出值． 试题解析：原式= ? =， 当x=1时,原式=.

    查看答案和解析>>

    同步练习册答案