
分式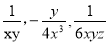 的最简公分母是________
的最简公分母是________
科目:初中数学 来源:黄金30题系列 八年级数学 大题好拿分 题型:解答题
因式分【解析】
①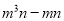 ,②
,②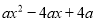 .
.
③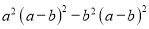 ,④
,④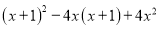 .
.
查看答案和解析>>
科目:初中数学 来源:湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷(含答案) 题型:解答题
在△ABC中,∠ACB=90°,P为BC中点,PD⊥AB于D,求证:AD2﹣BD2=AC2 .
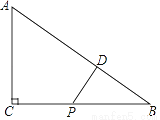
查看答案和解析>>
科目:初中数学 来源:湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷(含答案) 题型:单选题
直角三角形的周长为12cm,斜边长为5cm,则其面积为( )
A. 12cm2 B. 6cm2 C. 8cm2 D. 10cm2
B 【解析】 试题分析:设直角三角形的两条直角边长分别为a和b,根据直角三角形的周长及勾股定理即可得到关于a和b的方程组,再结合直角三角形的面积公式即可求得结果. 设直角三角形的两条直角边长分别为a和b,由题意得 ,解得 则 所以直角三角形的面积 故选B.查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年八年级(上)期末复习测试数学试卷 题型:解答题
如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
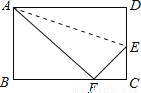
查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年八年级(上)期末复习测试数学试卷 题型:单选题
等边三角形的边长为2,则该三角形的面积为( )
A. 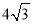 B.
B. 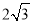 C.
C. 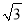 D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:填空题
若式子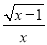 无意义,则x的取值范围是_____.
无意义,则x的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:解答题
阅读材料:
在一个三角形中,各边和它所对角的正弦的比相等, 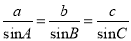 ,利用上述结论可以求解如下题目:
,利用上述结论可以求解如下题目:
在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.
【解析】
在△ABC中,∵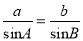
∴b= .
.
理解应用:
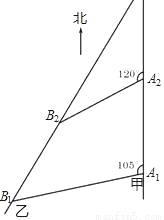
如图,甲船以每小时30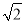 海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10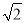 海里.
海里.
(1)判断△A1A2B2的形状,并给出证明;
(2)求乙船每小时航行多少海里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com