
已知实数a、b满足:ab=1且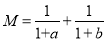 ,
, 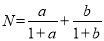 ,则M、N的关系为( )
,则M、N的关系为( )
A. M>N B. M<N C. M=N D. M、N的大小不能确定
C 【解析】先通分,再利用作差法可由= , =,因此可得M﹣N=﹣==,由ab=1,可得2﹣2ab=0,即M﹣N=0,即M=N. 故选:C. 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源:山东省2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
下列式子:① 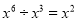 ;②
;②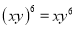 ;③
;③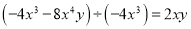 ;④
;④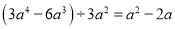 .其中计算不正确的有( )
.其中计算不正确的有( )
A. 3个 B. 2个 C. 1个 D. 0个
A 【解析】试题分析:①、同底数幂除法,底数不变,指数相减,原式=,则错误;②、积的乘方,原式=,则错误;③、根据同底数幂的除法分别进行计算,原式=1+2xy,则错误;④、计算正确,故选A.查看答案和解析>>
科目:初中数学 来源:湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷(含答案) 题型:填空题
如图,CE平分∠ACB,且CE⊥DB,∠DAB=∠DBA,又知AC=18, △CDB的周长为28,则BD的长为__________。
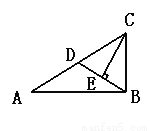
查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年八年级(上)期末复习测试数学试卷 题型:解答题
已知:如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF, 求证:△ABC≌△DEF.
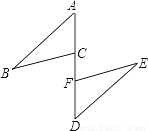
查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年八年级(上)期末复习测试数学试卷 题型:单选题
如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )

A.25° B.30° C.45° D.60°
B 【解析】考查直角三角形的性质,等边三角形的判定及图形折叠等知识的综合应用能力及推理能力.先根据图形折叠的性质得出BC=CE,再由直角三角形斜边的中线等于斜边的一半即可得出CE=AE,进而可判断出△BEC是等边三角形,由等边三角形的性质及直角三角形两锐角互补的性质即可得出结论. 【解析】 △ABC沿CD折叠B与E重合, 则BC=CE, ∵E为AB中点,△ABC是直角三角...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
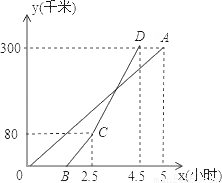
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:单选题
如图,已知DE∥BC,AB=AC,∠1=125°,则∠C的度数是( )
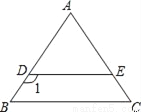
A. 55° B. 45° C. 35° D. 65°
A 【解析】∵∠1=125°,DE∥BC,∴∠B=180°–125°=55°,∵AB=AC,∴∠C=∠B=55°,故选A.查看答案和解析>>
科目:初中数学 来源:2017年江苏省苏州市中考数学模拟试卷(三) 题型:填空题
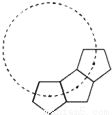
如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需_____个五边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com