
�۲����и�ʽ����չ��ʽ��
��a+b��2=a2+2ab+b2
��a+b��3=a3+3a2b+3ab2+b3
��a+b��4=a4+4a3b+6a2b2+4ab3+b4
��a+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
��
������루a+b��10��չ��ʽ�������ϵ���ǣ� ��
A. 36 B. 45 C. 55 D. 66
B ����������������������ܽ�õ�չ��ʽ�е�����ϵ�����ɣ� �������� �������� ��a+b��2=a2+2ab+b2�� ��a+b��3=a3+3a2b+3ab2+b3�� ��a+b��4=a4+4a3b+6a2b2+4ab3+b4�� ��a+b��5=a5+5a4b+10a3b2+10a2b3+5ab4+b5�� ��a+b��6=a6+6a5b+15a4b2+20a3b3+1...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�γ���2017-2018ѧ����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
�����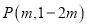 �ڵ������ޣ���ô
�ڵ������ޣ���ô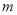 ��ȡֵ��Χ�ǣ� ����
��ȡֵ��Χ�ǣ� ����
A. 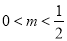 B.
B. 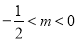 C.
C. 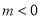 D.
D. 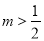
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����в�2017-2018ѧ����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ������
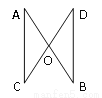
��ͼ����֪�߶�AB��CD�ཻ�ڵ�O���ҡ�A=��B��ֻ�貹��һ������_________�����С�AOC�ա�BOD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����������������2017���п���ѧһģ�Ծ� ���ͣ������
Ϊ��Ӧ�������������������塱�ĺ��٣�ijУ��չ���������������У���Ļ����У����������ƣ��������Ҫ�̻������Ϊ498m2 �� �̻�150m2��Ϊ�˸������ɸ����̻���������ÿ��Ĺ��������Ϊԭ����1.2�������һ����20������˸����̻������������̻�����ԭ�ƻ�ÿ����ɶ���m2��
�����̻�����ԭ�ƻ�ÿ�����22m2 �� ����������������� ��ԭ�ƻ�ÿ�����m2����ͨ��Ч�ʺ�ÿ������m2�����Ч��ǰ�̻����죬���Ч�ʺ��̻����죬����һ����20������˸����̻��������г����̣��ⷽ�̼������ԭ�ƻ�ÿ����ɵĹ�����. ��������� ���̻�����ԭ�ƻ�ÿ�����m2 �� ������ã� +=20�� ��ã� =22�� �����飺 =22��ԭ��ʽ���̵Ľ⣬...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����������������2017���п���ѧһģ�Ծ� ���ͣ������
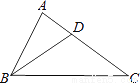
��ͼ��Rt��ABC�С�A=90�㣬��C=30�㣬BDƽ�֡�ABC����AC�߽��ڵ�D��AD=2�����D����BC�ľ�����________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����������������2017���п���ѧһģ�Ծ� ���ͣ���ѡ��
���м�����ȷ���ǣ� ��
A. ab•ab=2ab B. ��2a��3=2a3
C. 3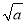 ��
��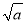 =3��a��0�� D.
=3��a��0�� D. 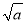 ?
?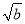 =
=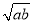 ��a��0��b��0��
��a��0��b��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ������
����ѧ�����κ�����ͼ���ƽ�ƣ��磺�����κ���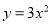 ��ͼ������ƽ��2����λ��������ƽ��4����λ����ͼ��ĺ�������ʽ��
��ͼ������ƽ��2����λ��������ƽ��4����λ����ͼ��ĺ�������ʽ��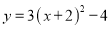 .��ȶ��κ�����ͼ���ƽ�ƣ����ǶԷ�����������ͼ�������Ƶı任��
.��ȶ��κ�����ͼ���ƽ�ƣ����ǶԷ�����������ͼ�������Ƶı任��
��1����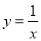 ��ͼ������ƽ��1����λ������ͼ��ĺ�������ʽΪ_______��������ƽ��1����λ������ͼ��ĺ�������ʽΪ_________��
��ͼ������ƽ��1����λ������ͼ��ĺ�������ʽΪ_______��������ƽ��1����λ������ͼ��ĺ�������ʽΪ_________��
��2������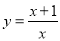 ��ͼ�����
��ͼ�����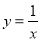 ��ͼ����____ƽ��____����λ�õ���
��ͼ����____ƽ��____����λ�õ��� 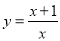 ��ͼ������ĸ�������������ͼ�������ı任�õ���
��ͼ������ĸ�������������ͼ�������ı任�õ���
��3��һ��أ�����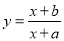 ��
��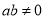 ����
����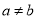 ����ͼ������ĸ�������������ͼ���������ı任�õ���
����ͼ������ĸ�������������ͼ���������ı任�õ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2018����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ���ѡ��
��ͼ����Rt��ABC�У���ACB=90�㣬BC=2��AB=4�������н�����ȷ���ǣ�������

A. tanB= B. tanA=
B. tanA= C. cosB=
C. cosB= D. sinA=
D. sinA=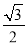
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ ������÷� ���ͣ������
��ͼ����A�Ƿ���������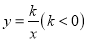 ͼ���ϵ�һ�㣬����A��AB��
ͼ���ϵ�һ�㣬����A��AB��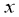 ���ڵ�B���ҡ�AOB�����Ϊ2����A������Ϊ
���ڵ�B���ҡ�AOB�����Ϊ2����A������Ϊ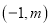 ��
��
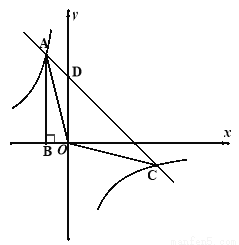
��1����m��k��ֵ��
��2����һ�κ���y=ax+3��ͼ����A����˫���ߵ���һ֧�ڵ�C����y���ڵ�D�����AOC�������
��3����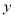 �����Ƿ���ڵ�P��ʹ�á�PAC�����Ϊ6��������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�����Ƿ���ڵ�P��ʹ�á�PAC�����Ϊ6��������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com