练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列计算正确的是（   ）

    A. ab•ab=2ab B. （2a）3=2a3

    C. 3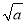﹣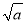=3（a≥0）  D. 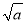?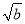=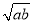（a≥0，b≥0）

    D 【解析】A、ab•ab=a2b2，故此选项错误；B、（2a）3=8a3，故此选项错误；C、3﹣=2（a≥0），故此选项错误；D、•=（a≥0，b≥0），正确， 故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省盐城市2017-2018学年八年级12月月考数学试卷 题型：单选题

    在实数0、π、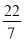、、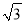﹣、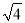3.1010010001中，无理数的个数有（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】无理数是无限不循环小数，根据无理数的定义可得在实数0、π、、、﹣、3.1010010001中，π、是无理数，故选B.

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市部2017-2018学年八年级（上）第一次月考数学试卷 题型：单选题

    已知△ABC≌△DEF，∠A=80°，∠E=40°，则∠F等于（ ）

    A. 80° B. 40° C. 60° D. 120°

    C 【解析】∵△ABC≌△DEF，∠A=80°， ∴∠D=∠A=80°. ∴∠F=180°-80°-40=60°. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：广西崇左市天等县2017年中考数学一模试卷 题型：解答题

    计算：|﹣3|+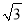（﹣π）0﹣2tan45°．

    2 【解析】试题分析： 代入45°角的正切值，结合0指数幂的意义，绝对值的意义计算即可； 试题解析： 原式=3+1﹣2×1=2.

    查看答案和解析>>

    科目：初中数学 来源：广西崇左市天等县2017年中考数学一模试卷 题型：单选题

    观察下列各式及其展开式：

    （a+b）2=a2+2ab+b2

    （a+b）3=a3+3a2b+3ab2+b3

    （a+b）4=a4+4a3b+6a2b2+4ab3+b4

    （a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5

    …

    请你猜想（a+b）10的展开式第三项的系数是（   ）

    A. 36 B. 45 C. 55 D. 66

    B 【解析】试题分析：归纳总结得到展开式中第三项系数即可． 【解析】 【解析】 （a+b）2=a2+2ab+b2； （a+b）3=a3+3a2b+3ab2+b3； （a+b）4=a4+4a3b+6a2b2+4ab3+b4； （a+b）5=a5+5a4b+10a3b2+10a2b3+5ab4+b5； （a+b）6=a6+6a5b+15a4b2+20a3b3+1...

    查看答案和解析>>

    科目：初中数学 来源：广西崇左市天等县2017年中考数学一模试卷 题型：单选题

    实数0是（   ）

    A. 有理数  B. 无理数    C. 正数   D. 负数

    A 【解析】试题分析：根据实数的分类可知： 0是有理数， 故选：A

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级上学期第三次月考数学试卷 题型：解答题

    解下列方程：

    (1)2x2－4x－1＝0(配方法)；

    (2)(x＋1)2＝6x＋6.

    (1)x1＝1＋，x2＝1－ (2) x1＝－1，x2＝5. 【解析】试题分析：（1）根据配方法解一元二次方程的方法，先移项，再加减一次项系数一半的平方，完成配方，再根据直接开平方法解方程即可； （2）根据因式分解法，先移项，再提公因式即可把方程化为ab=0的形式，然后求解即可. 试题解析：(1)由题可得，x2－2x＝，∴x2－2x＋1＝. ∴(x－1)2＝. ∴x－...

    查看答案和解析>>

    科目：初中数学 来源：湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷（含答案） 题型：解答题

    已知：如图，E，F是?ABCD的对角线AC上的两点，BE∥DF，求证：AF=CE．

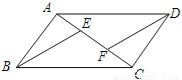
    参见解析． 【解析】利用平行四边形的性质证△BEC与△DFA全等，即可得出续论. 证明：在平行四边形ABCD中，∵AD∥BC，AD=BC， ∴∠ACB=∠CAD． 又∵BE∥DF， ∴∠BEC=∠DFA， 在△BEC与△DFA中， ， ∴△BEC≌△DFA， ∴AF=CE．

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 九年级数学 大题好拿分 题型：解答题

    如图，是由边长为1的小正方形构成的网格，各个小正方形的顶点称之为格点，点A、C、E、F均在格点上，根据不同要求，选择格点，画出符合条件的图形：

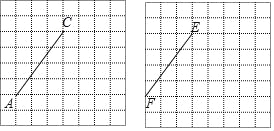
    （1）在图1中，画一个以AC为一边的△ABC，使∠ABC=45°（画出一个即可）；

    （2）在图2中，画一个以EF为一边的△DEF，使tan∠EDF=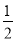，并直接写出线段DF的长．

    （1）画图见解析．（2）DF==4； 【解析】 试题分析：（1）利用网格特点，AB在水平格线上，BC为4×4的正方形的对角线； （2）由于tan∠EDF=，则在含∠D的直角三角形中，满足对边与邻边之比为1：2即可． 试题解析：（1）如图1，△ABC为所作； （2）如图2，△DEF为所作，DF==4．

    查看答案和解析>>

    同步练习册答案