练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    小明准备测量一段河水的深度，他把一根竹竿竖直插到离岸边1.5 m远的水底，竹竿高出水面0.5 m，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为（　　）

    A. 3 m B. 2.5 m C. 2.25 m D. 2 m

    D 【解析】设竹竿长x米，则水深（x-0.5）米，根据勾股定理可得x2=1.52+（x-0.5）2，解得，x=2.5，所以水深2.5-0.5=2米．故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年广东省韶关市南雄市中考数学模拟试卷 题型：单选题

    下列图形中，是中心对称图形，但不是轴对称图形的是（　　）

    A. 正方形 B. 矩形 C. 菱形 D. 平行四边形

    D 【解析】试题分析：A、B、C既是轴对称图形，也是中心对称图形；D．不是轴对称图形，只是中心对称图形． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型：填空题

    已知点A（－3，y1），B（－1，y2），C（2，y3）在抛物线y＝ x2上，则y1，y2，y3的大小关系系是__________________.

    y1>y3>y2 【解析】∵当x=?3时,y1=x2=9；当x=?1时,y2= x2=1；当x=2时,y3=x2=4， ∴y1>y3>y2. 故答案为：y1>y3>y2.

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期末测试 题型：解答题

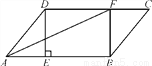
    如图，在?ABCD中，过点D作DE⊥AB于点E，点F在边CD上，CF＝AE，连接AF，BF.

    (1)求证：四边形BFDE是矩形；

    (2)若CF＝6，BF＝8，DF＝10，求证：AF是∠DAB的平分线．

    （1）证明见解析；（2）证明见解析. 【解析】试题分析：（1）根据已知条件易证四边形BFDE是平行四边形，再证明∠DEB=90°即可得结论；（2）根据已知条件证明AD＝DF，根据等腰三角形的性质可得∠DAF＝∠DFA；再由AB∥CD，可得∠DFA＝∠FAB.即可得∠DAF＝∠FAB，结论得证. 试题解析： 证明：（1）∵四边形ABCD是平行四边形， ∴AB∥CD，AB＝CD...

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期末测试 题型：填空题

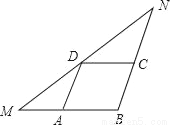
    如图，在△MBN中，已知：BM=6，BN=7，MN=10，点A，C，D分别是MB，NB，MN的中点，则四边形ABCD的周长是_____．

    13 【解析】∵点A，C，D分别是MB，NB，MN的中点， ∴CD∥AB，AD∥BC， ∴四边形ABCD为平行四边形， ∴AB=CD，AD=BC. ∵BM＝6，BN＝7，MN＝10，点A，C分别是MB，NB的中点， ∴AB=3，BC=3.5， ∴四边形ABCD的周长=（AB+BC）×2=（3+3.5）×2=13.

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期末测试 题型：单选题

    已知直角三角形的两直角边长分别为5和12，则此直角三角形斜边上的中线长为（）

    A. 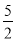B. 6 C. 13 D.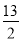

    D 【解析】已知直角三角形的两直角边长分别为5和12，根据勾股定理求得斜边为13，根据直角三角形斜边上的中线等于斜边的一半，得此直角三角形斜边上的中线长为，故选D.

    查看答案和解析>>

    科目：初中数学 来源：江西省2017-2018学年度八年级第三次月考数学试卷 题型：解答题

    某校初三年级春游，现有36座和42座两种客车供选择租用，若只租用36座客车若干辆，则正好坐满；若只租用42座客车，则能少租一辆，且有一辆车没有坐满，但超过30人；已知36座客车每辆租金400元，42座客车每辆租金440元.

    （1）该校初三年级共有多少人参加春游？

    （2）请你帮该校设计一种最省钱的租车方案．

    (1)288;(2)见解析 【解析】试题分析：（1）设租36座的车x辆，则租42座的客车（x-1）辆．根据不等关系“租42座客车，则能少租一辆，且有一辆车没有坐满，但超过30人”，列出不等式组，解不等式组即可．（2）根据（1）中求得的人数，进一步计算三种方案的费用：①只租36座客车；②只租42座客车；③合租两种车．再进一步比较得到结论即可． 试题解析： 【解析】 （1）设租36...

    查看答案和解析>>

    科目：初中数学 来源：江西省2017-2018学年度八年级第三次月考数学试卷 题型：单选题

    如图，AD平分∠BAC，AB=AC，连接BC，交AD于点E，下列说法正确的有（　　）

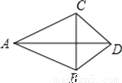
    ①∠BAC=∠ACB；②S四边形ABDC=AD•CE；③AB2+CD2=AC2+BD2；④AB﹣BD=AC﹣CD．

    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】如图，∵AD平分∠BAC，AB=AC， ∴AD⊥BC，CE=BE， ∴S四边形ABDC=S△ABD+S△ACD=AD×BE+AD×CE=AD（BE+CE）=AD×CE，②正确； ∵AD平分∠BAC， ∴∠BAD=∠CAD， 在△ABD与△ACD中， ， ∴△ABD≌△ACD（SAS）， ∴BD=CD， ∴③AB2+CD2=AC...

    查看答案和解析>>

    科目：初中数学 来源：山西省2017-2018学年八年级上期末模拟数学试卷 题型：填空题

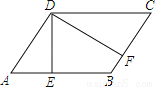
    如图，若?ABCD的周长为36cm，过点D分别作AB，BC边上的高DE，DF，且DE=4cm，DF=5cm，?ABCD的面积为 cm2．

    40 【解析】 试题分析：由?ABCD的周长为36cm，可得AB+BC=18cm①，又由过点D分别作AB，BC边上的高DE，DF，且DE=4cm，DF=5cm，由等积法，可得4AB=5BC②，继而求得答案． 【解析】 ∵?ABCD的周长为36cm， ∴AB+BC=18cm①， ∵过点D分别作AB，BC边上的高DE，DF，且DE=4cm，DF=5cm， ∴4AB...

    查看答案和解析>>

    同步练习册答案