练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

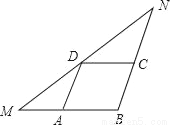
    如图，在△MBN中，已知：BM=6，BN=7，MN=10，点A，C，D分别是MB，NB，MN的中点，则四边形ABCD的周长是_____．

    13 【解析】∵点A，C，D分别是MB，NB，MN的中点， ∴CD∥AB，AD∥BC， ∴四边形ABCD为平行四边形， ∴AB=CD，AD=BC. ∵BM＝6，BN＝7，MN＝10，点A，C分别是MB，NB的中点， ∴AB=3，BC=3.5， ∴四边形ABCD的周长=（AB+BC）×2=（3+3.5）×2=13.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年广东省韶关市南雄市中考数学模拟试卷 题型：单选题

    若圆锥的底面半径为2cm，母线长为3cm，则它的侧面积为（　　）

    A. 2πcm2 B. 3πcm2 C. 6πcm2 D. 12πcm2

    C 【解析】【解析】 依题意知母线长=3cm，底面半径r=2cm， 则由圆锥的侧面积公式得S=πrl=π×2×3=6πcm 2． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型：填空题

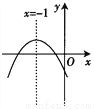
    y＝ax2＋bx＋c(a≠0)的图象如下图所示，那么下面五个代数式：①abc，②b2－4ac，③a－b＋c，④a＋b＋c，⑤ 2a－b中，值小于0的有________．（所有成立的序号）

    ①④ 【解析】①由抛物线的开口方向向下可推出a<0； 因为对称轴在y轴左侧,对称轴为x=?<0， 又因为a<0，b<0； 由抛物线与y轴的交点在y轴的负半轴上， ∴c<0， 故abc<0； ②抛物线与x轴有两个交点,b2?4ac>0； ③当x=?1时，a?b+c>0； ④当x=1时，y=a+b+c<0； ⑤对称轴x=?=?1，2a=b，2...

    查看答案和解析>>

    科目：初中数学 来源：山东省德州市2017-2018学年九年级上学期期中考试数学试卷 题型：单选题

    方程x（x-2）= 2 -x的解是（ ）

    A. 2 B. -2,1 C. －1 D. 2,－1

    D 【解析】试题分析：∵x（x-2）=2-x ∴x（x-2）+x-2=0 （x-2）（x+1）=0 x-2=0，x+1=0 解得：x1=2，x2=-1 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期末测试 题型：解答题

    已知：如图，在△ABC中，∠B＝30°，∠C＝45°，AC＝2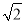，求S△ABC.

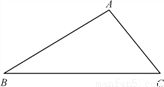
    2＋2 【解析】试题分析：作AD⊥BC于D，在Rt△ACD中，求得AD、CD的长；在Rt△ABD中，求得BD的长，继而求得BC的长，根据三角形的面积公式即可求得△ABC的面积. 试题解析： 作AD⊥BC于D， ∵∠C=45°，AC=， ∴AD=CD=2， 又∵在Rt△ABD中，∠B=30° ∴BD=AD=2. ∴BC=BD+CD=2+2 ∴． ...

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期末测试 题型：单选题

    小明准备测量一段河水的深度，他把一根竹竿竖直插到离岸边1.5 m远的水底，竹竿高出水面0.5 m，把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐，则河水的深度为（　　）

    A. 3 m B. 2.5 m C. 2.25 m D. 2 m

    D 【解析】设竹竿长x米，则水深（x-0.5）米，根据勾股定理可得x2=1.52+（x-0.5）2，解得，x=2.5，所以水深2.5-0.5=2米．故选D．

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期末测试 题型：单选题

    下列各组数不能作为直角三角形三边长的是（　　）

    A. 3，4，5 B. 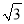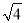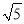， ， C. 0.3，0.4，0.5 D. 30，40，50

    B 【解析】选项A， ，三角形是直角三角形； 选项B， ，三角形不是直角三角形；选项C， ，三角形是直角三角形； 选项D， ，三角形是直角三角形；故选B ．

    查看答案和解析>>

    科目：初中数学 来源：江西省2017-2018学年度八年级第三次月考数学试卷 题型：填空题

    如图所示，在锐角三角形ABC中， 直线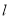为BC的垂直平分线,直线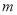为∠ABC的平分线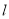， 与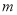相交于P点.若∠A=600, ∠ACP=240，则∠ABP的度数为_______.

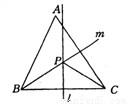
    32° 【解析】∵直线为∠ABC的角平分线， ∴∠ABP=∠CBP． ∵直线为BC的中垂线， ∴BP=CP， ∴∠CBP=∠BCP， ∴∠ABP=∠CBP=∠BCP， 在△ABC中，3∠ABP+∠A+∠ACP=180°， 即3∠ABP+60°+24°=180°， 解得∠ABP=32°．

    查看答案和解析>>

    科目：初中数学 来源：山西省2017-2018学年八年级上期末模拟数学试卷 题型：解答题

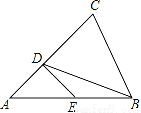
    如图所示，点D在AC上，点E在AB上，且AB=AC，BC=BD，AD=DE=EB，求∠A的度数．

    45°． 【解析】试题分析：由线段相等，可得对应角相等，通过转化，将∠A、∠ABC都与∠DBE建立联系，从而即可求解∠A的值． 试题解析：∵AB=AC， ∴∠ABC=∠C，又BC=BD， ∴∠BDC=∠C， ∵∠A+∠C+∠ABC=180°，∠DBC+∠C+∠BDC=180°， ∴∠DBC=∠A， ∵AD=DE=EB， ∴∠A=∠AED，∠EDB=∠...

    查看答案和解析>>

    同步练习册答案