
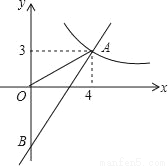
��ͼ��һ�κ���y=kx+b��ͼ��ֱ��뷴��������y=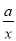 ��ͼ���ڵ�һ�����ڵ�A��4��3������y��ĸ����ύ�ڵ�B����OA=OB��
��ͼ���ڵ�һ�����ڵ�A��4��3������y��ĸ����ύ�ڵ�B����OA=OB��
��1������y=kx+b��y=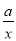 �ı���ʽ��
�ı���ʽ��
��2����֪��C��0��5�������ڸ�һ�κ���ͼ����ȷ��һ��M��ʹ��MB=MC�����ʱ��M�����꣮

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����ػ�ͤ��2017~2018ѧ����꼶��ѧ���ϣ���ĩ���ģ���� ���ͣ������
��֪����x ��һԪ���η���x2��3x��m��0����������ȵ�ʵ����x1��x2��
��1����m ��ȡֵ��Χ��
��2����x1��1ʱ������һ��x,2��ֵ��
��1��m<����2��x2��2�� �������������������1�����ø���ϵ���Ĺ�ϵ��.(2)����Τ�ﶨ��������ֵ. ��������� ��1��������ã���>0������9��4m>0�� ��m<�� ��2����x1+x2=3����x2��3��x1��3��1��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ����ĩ��ϰ�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ��AB��AC��A��BD��CD��D����AC=DB�������н����в���ȷ���ǣ�������
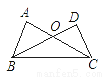
A. ��A=��D B. ��ABC=��DCB C. OB=OD D. OA=OD
C �������������������AB��AC��A��BD��CD��D ���A=��D=90�㣨A��ȷ�� �֡�AC=DB��BC=BC ���ABC�ա�DCB ���ABC=��DCB��B��ȷ�� ��AB=CD �֡ߡ�AOB=��C ���AOB�ա�DOC ��OA=OD��D��ȷ�� C��OD��OB���Ƕ�Ӧ�ߣ�����ȣ� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�������п���ѧģ���Ծ���4�·ݣ� ���ͣ���ѡ��
��֪�����ߺ�ֱ��l��ͬһֱ������ϵ�е�ͼ����ͼ��ʾ�������ߵĶԳ���Ϊֱ��x=��1��P1��x1��y1����P2��x2��y2�����������ϵĵ㣬P3��x3��y3����ֱ��l�ϵĵ㣬��x3����1��x1��x2����y1��y2��y3�Ĵ�С��ϵ�ǣ�������
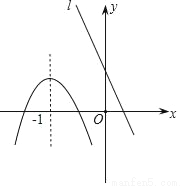
A. y1��y2��y3 B. y2��y3��y1 C. y3��y1��y2 D. y2��y1��y3
D ����������Ϊ�����ߵĶԳ���Ϊֱ��x=-1���������£�P1��x1��y1����P2��x2��y2�����������ϵĵ㣬��-1��x1��x2�����ݶ��κ��������ʣ��ڶԳ�����Ҳ࣬y��x���������С���ɵ�y2�� y1��P3��x3��y3����ֱ��l�ϵĵ㣬ֱ��y��x���������С����x3��-1����ͼ���֪��ֱ����x3��Ӧ�ĺ���ֵy3����-1��Ӧ�ĺ���ֵ������x=-1ʱ�������ߵĶ�����ߣ��ɵ�y3�������y2��...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�������п���ѧģ���Ծ���4�·ݣ� ���ͣ���ѡ��
�ڢ٩�a5•����a��2���ڣ���a6���£���a3�����ۣ���a2��3•��a3��2����[������a��2]5�м�����Ϊ��a10���У�������
A. �٢� B. �ۢ� C. �ڢ� D. ��
D ����������ԭʽ=?����ԭʽ=�� ��ԭʽ= ����ԭʽ=�� ��ѡD�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�����н�������ѧУ�п���ѧģ���Ծ� ���ͣ������
���㣺���Щ�4��0+|3��tan60��|����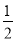 ����2+
����2+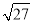 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�����н�������ѧУ�п���ѧģ���Ծ� ���ͣ���ѡ��
С���ڴ�����ʱ��Ϊʹ��ǡ���ܹ���������0.8�ף��������ڶԷ���������5��λ���ϣ���֪���Ļ���߶���2.4�ף�����Ӧվ�������ģ�������
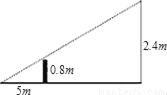
A. 7.5�״� B. 8�״� C. 10�״� D. 15�״�
C ���������������������Ӧվ��������x�״�����������ã� ����ã�x=10�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�������п���ѧģ���Ծ� ���ͣ������
��2014•����ģ�⣩��ͼ��һ��ȱ������ε�ľ�壬�߳�Ϊ1���ֽ�ľ����ˮƽ�߷�������ôB��ӿ�ʼ���������߹���·������Ϊ ��
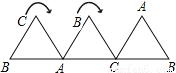
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ����ѧ���꼶��ͬ����ϰ��2.2.2ƽ����3 ���ͣ������
���ɲ����룺
(1) 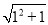 ����������Ϊ____��
����������Ϊ____��
(2) 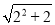 ����������Ϊ____��
����������Ϊ____��
(3) 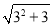 ����������Ϊ____��
����������Ϊ____��
(4)���룺��nΪ������ʱ�� 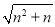 ����������Ϊ____��С������Ϊ____��
����������Ϊ____��С������Ϊ____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com