练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

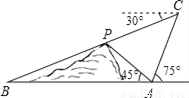
    如图，在小山的东侧A庄，有一热气球，由于受西风的影响，以每分钟35米的速度沿着与水平方向成75度角的方向飞行，40分钟时到达C处，此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上，同时测得B庄的俯角为30度，又在A庄测得山顶P的仰角为45度，求A庄与B庄的距离___________，山高__________．

    米； 700（）米 【解析】试题解析：如图，过点A作AD⊥BC，垂足为D， 在Rt△ACD中，∠ACD=75°-30°=45°， AC=35×40=1400（米）， ∴AD=AC•sin45°=700（米）． 在Rt△ABD中，∠B=30°， AB=2AD=1400（米）． 又过点P作PE⊥AB，垂足为E， 则AE=PE•tan45°=PE， ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年湖北省黄石市中考数学模拟试卷 题型：单选题

    如图，在△ABC中，BC=8，AB的中垂线交BC于D，AC的中垂线交BC于E，则△ADE的周长等于（　　）

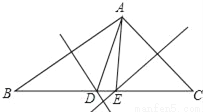
    A. 8 B. 4 C. 12 D. 16

    A 【解析】试题解析：∵AB的中垂线交BC于D，AC的中垂线交BC于E， ∴DA=DB，EA=EC， 则△ADE的周长=AD+DE+AE=BD+DE+EC=BC=8， 故选A．

    查看答案和解析>>

    科目：初中数学 来源：广东省2017年中考数学一模试卷 题型：填空题

    3 120 000用科学记数法表示为________．

    3.12×106 【解析】3 120 000用科学记数法表示为3.12×106. 故答案为3.12×106.

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学三模试卷 题型：解答题

    为了普及环保知识，增强环保意识，某中学组织了环保知识竞赛，初中三个年级根据初赛成绩分别选出了10名同学参加决赛，这些选手的决赛成绩（满分为100分）如下表所示：

    年级

    决赛成绩（单位：分）

    七年级

    80

    86

    88

    80

    88

    99

    80

    74

    91

    89

    八年级

    85

    85

    87

    97

    85

    76

    88

    77

    87

    88

    九年级

    82

    80

    78

    78

    81

    96

    97

    88

    89

    86

    (1)请你填写下表：

    年级

    平均数

    众数

    中位数

    七年级

    85.5

    87

    八年级

    85.5

    85

    九年级

    84

    (2)请从以下两个不同的角度对三个年级的决赛成绩进行分析：

    ①从平均数和众数相结合看（分析哪个年级成绩好些）；

    ②从平均数和中位数相结合看（分析哪个年级成绩好些）

    ③如果在每个年级分别选出3人参加决赛，你认为哪个年级的实力更强一些？并说明理由.

    （1）填表见解析（2）①八年级②七年级③九年级 【解析】（1）平均数的计算方法是求出所有数据的和，然后除以数据的总个数．对于中位数， 因图中是按从小到大的顺序排列的，所以只要找出最中间的一个数（或最中间的两个数）即 可，本题是最中间两个数的平均数．对于众数是出现次数最多的数据； （2）可由（1）得出的表格，将三个年级的平均数，众数和中位数进行比较即可得出正确的 结论；...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学三模试卷 题型：单选题

    某次“迎奥运”知识竞赛中共20道题，对于每一道题，答对得10分，答错或不答扣5分，选手至少要答对（　　）道题，其得分才会不少于95分？

    A. 14 B. 13 C. 12 D. 11

    B 【解析】试题解析：设答对x道，则答错或不答的题目就有20-x个． 即10x-5（20-x）≥95 去括号：10x-100+5x≥95 ∴15x≥195 x≥13 因此选手至少要答对13道． 故应选B．

    查看答案和解析>>

    科目：初中数学 来源：江苏省徐州市丰县2018届九年级上学期第二次月考数学试卷 题型：解答题

    如图，抛物线y=ax2-6ax+6(a≠0)与x轴交于点A(8,0)，与y轴交于点B，在X轴上有一动点E(m,0)(0＜m＜8)，过点E作x轴的垂线交直线AB于点N，交抛物线于点P,过点P作PM⊥AB于点M．

    （）分别求出直线AB和抛物线的函数表达式；

    （）设△PMN的面积为S1，△AEN的面积为S2，若S1：S2=36：25，求m的值；

    （）如图2，在（）条件下，将线段OE绕点O逆时针旋转得到OE＇，旋转角为α(0°＜α＜90°)，连接E＇A、E＇B．

    ①在x轴上找一点Q，使△OQE＇∽△OE＇A，并求出Q点的坐标；

    ②求BE＇+AE＇的最小值．

    （1）； ；（2）4；（3）①，②． 【解析】分析：（1）把点A（8，0）代入抛物线y=ax²-6ax+6，可求得a的值，从而可得到抛物线的解析式，然后求得点A和点B的坐标，最后利用待定系数法可求得直线AB的解析式； （2）E（m，0），则N（m，-m+6），P（m， +6），然后证明△ANE∽△ABO，依据相似三角形的性质可求得AN的长，接下来，再证明△NMP∽△NEA，然后依据相似...

    查看答案和解析>>

    科目：初中数学 来源：江苏省徐州市丰县2018届九年级上学期第二次月考数学试卷 题型：填空题

    如图，在△ABC中，AB＝9，AC＝6，BC＝12，点M在边AB上，AM＝3，过点M作直线MN与边AC交于点N，使截得的三角形与原三角形ABC相似，则MN的长为_____．

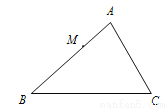
    4或6 【解析】作出图形，然后分①点N在AC上，分AM和AB与AC是对应边两种情况，利用相似三角形对应边成比例列式求解即可；②点N在BC上，求出BM，再分BM和AB与BC是对应边，利用相似三角形对应边成比例列式求解即可． 【解析】 如图所示， ①点N在AC上，若AM和AB是对应边， ∵△AMN∽△ABC， ∴，即， 解得MN=4， 若AM和AC是对应边， ∵△AMN∽...

    查看答案和解析>>

    科目：初中数学 来源：2017广东省深圳市中考数学模拟试卷（三） 题型：解答题

    把下列各数填在相应的大括号内：

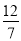    ，﹣3.1416，0，2017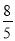，﹣，﹣0.23456，10%，10.1，0.67，﹣89

    正数集合：{　 　…}

    整数集合：{　 　…}

    分数集合：{　 　…}．

    详见解析. 【解析】试题分析：根据正数、整数、分数的定义即可解决问题. 试题解析：正数集合：{，2017，10%，10.1，0.67…} 整数集合：{0，2017，﹣89…} 分数集合：{，﹣3，1416，﹣，﹣0.23456，10%，10.1，0.67…}．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年陕西省七年级（下）第二次测验数学试卷 题型：单选题

    我国在2009到2011三年中，各级政府投入医疗卫生领域资金达8500亿元人民币．将“8500亿元”用科学记数法表示为（　　）

    A. 8.5×1010元 B. 8.5×1011元 C. 0.85×1011元 D. 0.85×1012元

    B 【解析】由科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．因此8500=850000000000= 8.5×1011. 故选：B. 此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，...

    查看答案和解析>>

    同步练习册答案