
把下列各数填在相应的大括号内:
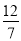 ,﹣3.1416,0,2017,﹣
,﹣3.1416,0,2017,﹣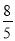 ,﹣0.23456,10%,10.1,0.67,﹣89
,﹣0.23456,10%,10.1,0.67,﹣89
正数集合:{ …}
整数集合:{ …}
分数集合:{ …}.
详见解析. 【解析】试题分析:根据正数、整数、分数的定义即可解决问题. 试题解析:正数集合:{,2017,10%,10.1,0.67…} 整数集合:{0,2017,﹣89…} 分数集合:{,﹣3,1416,﹣,﹣0.23456,10%,10.1,0.67…}. 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源:2016-2017学年内蒙古乌海市七年级(下)期末数学试卷 题型:单选题
如图AB∥CD可以得到( )
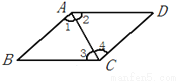
A. ∠1=∠2 B. ∠2=∠3 C. ∠1=∠4 D. ∠3=∠4
C 【解析】试题解析:A、∠1与∠2不是两平行线AB、CD形成的角,故A错误; B、∠3与∠2不是两平行线AB、CD形成的内错角,故B错误; C、∠1与∠4是两平行线AB、CD形成的内错角,故C正确; D、∠3与∠4不是两平行线AB、CD形成的角,无法判断两角的数量关系,故D错误. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年湖北省黄冈市中考数学三模试卷 题型:填空题
如图,在小山的东侧A庄,有一热气球,由于受西风的影响,以每分钟35米的速度沿着与水平方向成75度角的方向飞行,40分钟时到达C处,此时气球上的人发现气球与山顶P点及小山西侧的B庄在一条直线上,同时测得B庄的俯角为30度,又在A庄测得山顶P的仰角为45度,求A庄与B庄的距离___________,山高__________.
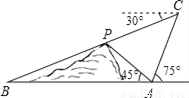
查看答案和解析>>
科目:初中数学 来源:江苏省徐州市丰县2018届九年级上学期第二次月考数学试卷 题型:单选题
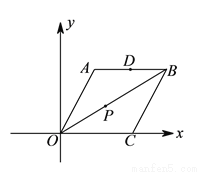
如图,菱形OABC在平面直角坐标系的位置如图所示,点B的坐标为(9,3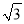 ),点D是AB的中点,点P在OB上,则△ADP的周长最小值为( )
),点D是AB的中点,点P在OB上,则△ADP的周长最小值为( )
A. 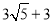 B.
B. 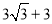 C.
C. 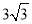 D.
D. 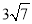
查看答案和解析>>
科目:初中数学 来源:2017广东省深圳市中考数学模拟试卷(三) 题型:解答题
已知|a+3|+|b﹣5|=0,求:
(1)a+b的值;
(2)|a|+|b|的值.
(1)a+b=2;(2)8. 【解析】根据非负数的性质列式求出a、b的值,然后分别代入代数式进行计算即可得解. (1)由题意得,a+3=0,b﹣5=0, 解得a=﹣3,b=5, 所以,a+b=﹣3+5=2; (2)|a|+|b|=|﹣3|+|5|=3+5=8.查看答案和解析>>
科目:初中数学 来源:2017广东省深圳市中考数学模拟试卷(三) 题型:填空题
在数轴上,﹣4与之﹣6间的距离是 .
2. 【解析】根据数轴上两点间的距离等于这两点表示的两个数的差的绝对值,即较大的数减去较小的数, 则-4与-6之间的距离是-4-(-6)=2. 故答案为:2.查看答案和解析>>
科目:初中数学 来源:2017广东省深圳市中考数学模拟试卷(三) 题型:单选题
为计算简便,把(﹣2.4)﹣(﹣4.7)﹣(+0.5)+(+3.4)+(﹣3.5)写成省略加号的和的形式,并按要求交换加数的位置正确的是( )
A. ﹣2.4+3.4﹣4.7﹣0.5﹣3.5 B. ﹣2.4+3.4+4.7+0.5﹣3.5
C. ﹣2.4+3.4+4.7﹣0.5﹣3.5 D. ﹣2.4+3.4+4.7﹣0.5+3.5
C 【解析】试题分析:(-2.4)-(-4.7)-(+0.5)+(+3.4)+(-3.5)写成省略加号的和的形式,-2.4+4.7-0.5+3.4-3.5,为计算方便则-2.4+3.4+4.7-0.5-3.5查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:填空题
纽约与北京的时差为﹣13h,李伯伯在北京乘坐中午十二点的航班飞行约20h到达纽约,那么李伯伯到达纽约时间是_____点.
19 【解析】根据纽约与北京的时差为﹣13h,可列式求解为:12+20﹣13=32﹣13=19,所以李伯伯到达纽约时间是19点,即晚上7点. 故答案为:19.查看答案和解析>>
科目:初中数学 来源:安徽省16-17学年度第一学期七年级数学期末考试卷 题型:填空题
若5xm+1y5与3x2y2n+1是同类项,则m=________,n=________.
1 2 【解析】根据同类项的定义,得出关于m,n的方程,求出m,n的值. 【解析】 ∵单项式5xm+1y5与3x2y2n+1是同类项, ∴m+1=2,m=1,2n+1=5, n=2, 故答案为:1,2. “点睛”本题考查了同类项的知识,解答本题的关键是掌握同类项定义中的两个“相同”:相同字母的指数相同.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com