
已知x=1是关于x的一元二次方程x2﹣4mx+m2=0的根,求代数式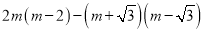 的值.
的值.
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:填空题
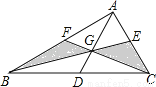
如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是______.
查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:解答题
青青书店购进了一批进价为每本20元的中华传统文化丛书. 在销售的过程中发现,这种图书每天的销售数量y(本)与销售单价x(元)满足一次函数关系:y=-3x+108(20<x<36). 如果销售这种图书每天的利润为p(元),那么销售单价定为多少元时,每天获得的利润最大?最大利润是多少?
销售单价定为28元时,每天获得的利润最大,最大利润是192元. 【解析】试题分析:由利润=每本书的利润×数量就可以得出解析式,再根据函数的性质即可得到最大利润. 试题解析:p=(x-20)(-3x+108)=-3x2+168x-2160=-3(x-28)2+192, ∵20查看答案和解析>>
科目:初中数学 来源:北京四中2018届上学期初中九年级期中考试数学试卷 题型:单选题
若A(1,y1),B(2,y2)两点都在反比例函数y=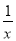 的图象上,则y1与y2的大小关系是( ).
的图象上,则y1与y2的大小关系是( ).
A. y1< y2 B. y1= y2 C. y1> y2 D. 无法确定
C 【解析】∵A(1,y1),B(2,y2)两点都在反比例函数y=的图象上, ∴1? y1=1,2? y2=1, 解得:y1=1, y2=, ∵1>, ∴y1>y2. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:解答题
如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数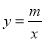 的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.
的图象交于C、D两点,DE⊥x轴于点E,已知C点的坐标是(6,﹣1),DE=3.
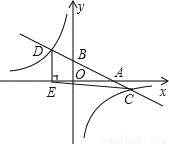
(1)求反比例函数与一次函数的解析式;
(2)求△CDE的面积.
(1)y=﹣,y=﹣x+2;(2)12. 【解析】试题分析: 分析题意,已知点在反比例函数的图象上,将点坐标代入反比例函数的解析式中即可得到的值,再由的长度求出点D的坐标;把两点的坐标代入一次函数即可求得一次函数的解析式. 过C作CH⊥轴于点H,根据 S△CDE=S△CAE+S△DAE,即可求出面积. 试题解析:(1)∵点在反比例图象上, ∴将代入反比例解析式得: 即 ...查看答案和解析>>
科目:初中数学 来源:2017年甘肃省张掖市中考数学三模试卷 题型:单选题
已知点A,B分别在反比例函数y=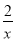 (x>0),y=
(x>0),y=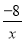 (x>0)的图象上且OA⊥OB,则tanB为( )
(x>0)的图象上且OA⊥OB,则tanB为( )
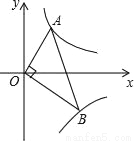
A. 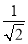 B.
B. 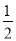 C.
C. 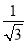 D.
D. 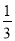
查看答案和解析>>
科目:初中数学 来源:2017年福建省分校九年级数学综合试卷(二) 题型:填空题
如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____________,使△AEH≌△CEB.
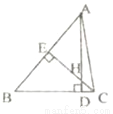
查看答案和解析>>
科目:初中数学 来源:2017年黑龙江省大庆市中考数学三模试卷 题型:解答题
学校为统筹安排大课间体育活动,在各班随机选取了一部分学生,分成四类活动:“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查,整理收集到的数据,绘制成如下的两幅统计图.
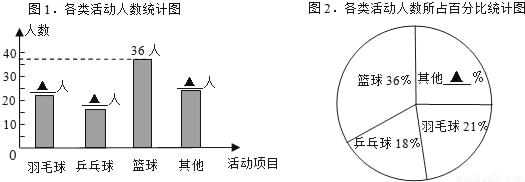
(1)学校采用的调查方式是 ;学校共选取了 名学生;
(2)补全统计图中的数据:条形统计图中羽毛球 人、乒乓球 人、其他 人、扇形统计图中其他 %;
(3)该校共有1200名学生,请估计喜欢“乒乓球”的学生人数.
(1)抽样调查,100;(2)21,18,25,25%;(3)估计喜欢“乒乓球”的学生人数有180人. 【解析】试题分析:(1)属于抽样调查.根据所占人数÷总人数×100%=百分比,计算即可; (2)根据百分比公式计算即可; (3)用样本估计总体的思想解决问题; 试题解析:(1)学校采用的调查方式是抽样调查, 总人数=36÷36%=100(名), 故答案为:抽样...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com