
如图所示,一只蚂蚁从点O出发,沿北偏东45°的方向爬行2.5cm,碰到障碍物(记作点B)后,再向北偏西60°的方向爬行3cm(此时位置记作点C).
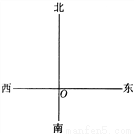
(1)画出蚂蚁的爬行路线;
(2)求出∠OBC的度数.
(1)图形见解析(2)75° 【解析】试题分析:(1)根据题意,结合方向角,直接可画图; (2)根据方位角,结合三角形的内角和求解即可. 试题解析:(1)如图所示,OBC为蚂蚁爬行的路线. (2)因为点B在点O的北偏东45°方向上,所以∠OBD=∠BOE=45°.又因为点C在点B的北偏西60°方向上,所以∠CBD=30°.又因为∠OBC=∠CBD+∠OBD,所以∠OBC=4...科目:初中数学 来源:贵州省黔南州2017-2018学年八年级上学期期末联考数学试卷 题型:解答题
先化简,再求值  ,其中x满足
,其中x满足 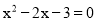 .
.
查看答案和解析>>
科目:初中数学 来源:山东省青岛市2017-2018学年上学期期末考试八年级数学试卷 题型:填空题
若一个多边形的内角和是它的外角和的3倍,则这个多边形是 边形..
八 【解析】设这个多边形是n边形,由题意得, (n-2) ×180=360×3, 解之得 n=8. 故答案为:八查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2018届九年级上学期期末考试数学试卷 题型:单选题
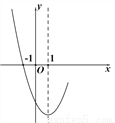
抛物线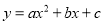 的部分图象如图所示(对称轴是
的部分图象如图所示(对称轴是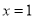 ),若
),若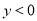 ,则
,则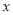 的取值范围是( )
的取值范围是( )
A. 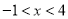 B.
B. 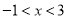 C.
C. 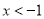 或
或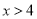 D.
D. 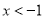 或
或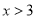
查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2018届九年级上学期期末考试数学试卷 题型:单选题
下列标志既是轴对称图形又是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:单选题
已知三条不同的射线OA、OB、OC有下列条件:①∠AOC=∠BOC ②∠AOB=2∠AOC ③∠AOC+∠COB=∠AOB ④∠BOC=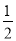 ∠AOB,其中能确定OC平分∠AOB的有( )
∠AOB,其中能确定OC平分∠AOB的有( )
A. 4个 B. 3个 C. 2个 D. 1个
D 【解析】如图, 根据角平分线的意义,可由∠AOC=∠BOC,知OC是∠AOB的平分线; 如图, 此时,∠AOB=2∠BOC,∠BOC=∠AOB,但OC不是∠AOB的平分线; 由于∠AOC+∠COB=∠AOB,但是∠AOC与∠COB不一定相等,所以OC不一定是∠AOB的平分线. 所以只有①能说明OC是∠AOB的角平分线. 故选:D.查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:填空题
如果∠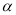 和∠
和∠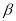 互补,且∠
互补,且∠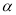 >∠
>∠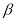 ,则下列表示的式子:①90°-∠
,则下列表示的式子:①90°-∠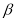 ②∠
②∠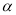 -90°③
-90°③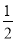 (∠
(∠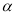 +∠
+∠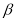 ) ④
) ④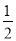 (∠
(∠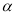 -∠
-∠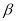 ),其中,能表示∠
),其中,能表示∠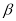 的余角的是____________(填序号).
的余角的是____________(填序号).
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:填空题
在Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的外接圆的半径是 .
5 【解析】分析:首先根据勾股定理,得其斜边是10,再根据直角三角形的外接圆的半径是斜边的一半,得其半径是5. 本题解析:∵∠C=90°,AC=6,BC=8, ∴BA=10, ∴其外接圆的半径为5.故答案为:5.查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
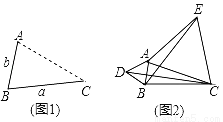
(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
①填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB、AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com