练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列图形中，∠1与∠2是对顶角的是( )

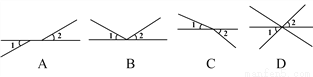
    A. A B. B C. C D. D

    D 【解析】A.∠1与∠2不是对顶角，故本选项错误； B.∠1与∠2不是对顶角，故本选项错误； C.∠1与∠2不是对顶角，故本选项错误； D.∠1与∠2是对顶角，故本选项正确； 故选：D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省长沙市2017-2018学年九年级（上）第一次月考数学试卷 题型：解答题

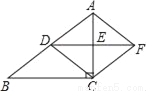
    如图，在Rt△ABC中，∠ACB=90°，D、E分别为AB、AC边上的中点，连接DE，将△ADE绕点E旋转180°得到△CFE，连接AF、CD．

    （1）求证：四边形ADCF是菱形；

    （2）若BC=8，AC=6，求四边形ABCF的周长．

    （1）证明见解析；（2）四边形ABCF的周长为28. 【解析】试题分析：（1）根据旋转可得AE=CE，DE=EF，可判定四边形ADCF是平行四边形，然后证明DF⊥AC，可得四边形ADCF是菱形； （2）首先利用勾股定理可得AB长，再根据中点定义可得AD=5，根据菱形的性质可得AF=FC=AD=5，进而可得答案． 试题解析：（1）∵将△ADE绕点E旋转180°得到△CFE， ...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.1.1 相交线与平行线 同步练习 题型：解答题

    将一张长方形纸片按图中的方式折叠,BC,BD为折痕,求∠CBD的大小.

    90°. 【解析】试题分析：∵折叠角相等，∴∠ABC=∠A′BC,∠EBD=∠E′BD,∴∠CBD=∠A′BC+∠E′BD=（∠ABA′+∠EBE′）=×180º=90º．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步练习题 含答案 题型：解答题

    如图，直线AB、CD相交于点O，OE平分∠BOC，∠BOC＝70°，OF是OE的反向延长线．

    (1)求∠DOF与∠BOF的度数；

    (2)OF平分∠AOD吗？为什么？

    (1)∠DOF＝35°，∠BOF＝145° (2)OF平分∠AOD. 【解析】试题分析：（1）根据角平分线的定义，可求得∠BOE=∠COE==35°，再根据对顶角的性质及邻补角的定义即可求得∠DOF与∠BOF的度数； （2）根据OF分∠AOD的两部分角的度数即可说明． 试题解析：（1）∵OE平分∠BOC， ∴∠BOE=∠COE=∠BOC=×70°=35°， ∴∠DOF...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步练习题 含答案 题型：单选题

    数学课上，同学们在练习过点B作线段AC所在直线的垂线段，正确的是( )

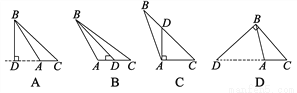
    A. A B. B C. C D. D

    A 【解析】A.根据垂线段的定义，故A正确； B.BD不垂直AC，所以错误； C.是过点D作的AC的垂线，所以错误； D.过点C作的BD的垂线，也错误. 故选：A.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型：填空题

    如图，直线AB、CD相交于点O，若∠1∶∠2＝1∶4，则∠1＝___，∠3＝______.

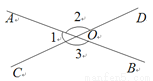
    36° 144° 【解析】设∠1=x，∠2=4x，根据题意得： x+4x=180°， 解得：x=36°， ∴∠1=36°，∠2=4×36°=144°， ∴∠3=∠2=144°， 故答案为：36°；144°．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型：单选题

    如图，AB⊥AC，AD⊥BC，垂足分别为A，D，则图中能表示点到直线距离的线段共有（ ）

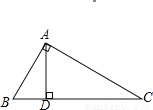
    A．2条 B．3条 C．4条 D．5条

    D. 【解析】 试题分析：如图所示，根据点到直线的距离就是这个点到这条直线垂线段的长度，可知线段AB是点B到AC的距离，线段CA是点C到AB的距离，线段AD是点A到BC的距离，线段BD是点B到AD的距离，线段CD是点C到AD的距离，所以图中能表示点到直线距离的线段共有5条．故答案选D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.3 多项式与多项式相乘 同步练习 题型：填空题

    已知m+n=mn,则(m-1)(n-1)=_______.

    1 【解析】试题分析：根据乘法公式多项式乘以多项式，用第一个多项式的每一项乘以第二个多项式的每一项，可求mn-m-n+1=mn-（m+n）+1，直接代入m+n=mn可求得1.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.2 单项式与多项式相乘 同步练习 题型：单选题

    要使x(x+a)+3x-2b=x2+5x+4成立,则a,b的值分别为(　　)

    A. -2,-2 B. 2,2 C. 2,-2 D. -2,2

    C 【解析】【解析】 ∵x（x+a）+3x-2b=x2+5x+4恒成立， ∴x2+（a+3）x-2b=x2+5x+4， ∴ a+3＝5，?2b＝4 解得 a＝2，b＝?2 ． 故选C．

    查看答案和解析>>

    同步练习册答案