练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，直线AB、CD相交于点O，OE平分∠BOC，∠BOC＝70°，OF是OE的反向延长线．

    (1)求∠DOF与∠BOF的度数；

    (2)OF平分∠AOD吗？为什么？

    (1)∠DOF＝35°，∠BOF＝145° (2)OF平分∠AOD. 【解析】试题分析：（1）根据角平分线的定义，可求得∠BOE=∠COE==35°，再根据对顶角的性质及邻补角的定义即可求得∠DOF与∠BOF的度数； （2）根据OF分∠AOD的两部分角的度数即可说明． 试题解析：（1）∵OE平分∠BOC， ∴∠BOE=∠COE=∠BOC=×70°=35°， ∴∠DOF...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级下册第一章1.3同底数幂的除法课时练习 题型：单选题

    (x+y)5÷(x+y)3等于（ ）.

    A. 7(x+y)(x+y) B. 2(x+y) C. (x+y)2 D (x+y)

    C 【解析】试题解析：(x+y)5÷(x+y)3 =(x+y)2，故C项正确. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学七年级下册 第1章 整式的乘除 章节检测题 题型：填空题

    地震中里氏震级增加1级，释放的能量增大到原来的32倍，那么里氏　 　级地震释放的能量是3级地震释放能量的324倍．

    7 【解析】设里氏n级地震释放的能量是3级地震释放能量的324倍，根据题意得出方程32n﹣1=323﹣1×324，求出方程的解即可． 【解析】 设里氏n级地震释放的能量是3级地震释放能量的324倍， 则32n﹣1=323﹣1×324， 32n﹣1=326， n﹣1=6， n=7． 故答案为：7．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.1.1 相交线与平行线 同步练习 题型：单选题

    如图，直线AB，CD相交于点O，因为∠1＋∠3＝180°，∠2＋∠3＝180°，所以∠1＝∠2，其推理依据是（　　）

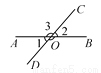
    A. 同角的余角相等 B. 对顶角相等 C. 同角的补角相等 D. 等角的补角相等

    C 【解析】根据同角的补角相等推出即可． 答：∵∠1+∠3=180°,∠2+∠3=180°， ∴∠1=∠2(同角的补角相等)， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.1.1 相交线与平行线 同步练习 题型：单选题

    如图,下列各组角中,是对顶角的一组是(　　)

    A. ∠1和∠2 B. ∠3和∠5 C. ∠3和∠4 D. ∠1和∠5

    B 【解析】试题分析：根据对顶角的定义，首先判断是否由两条直线相交形成，其次再判断两个角是否有公共边，没有公共边有公共顶点的是对顶角． 【解析】 由对顶角的定义可知：∠3和∠5是一对对顶角， 故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步练习题 含答案 题型：单选题

    如图，AD⊥BD，CD⊥BC，AB＝5cm，BC＝3cm，则线段BD的长度的取值范围是( )

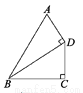
    A. 大于3cm B. 小于5cm C. 大于3cm或小于5cm D. 大于3cm且小于5cm

    D 【解析】∵AD⊥BD，BC⊥CD，AB=5cm，BC=3cm， ∴BC

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步练习题 含答案 题型：单选题

    下列图形中，∠1与∠2是对顶角的是( )

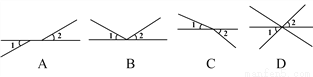
    A. A B. B C. C D. D

    D 【解析】A.∠1与∠2不是对顶角，故本选项错误； B.∠1与∠2不是对顶角，故本选项错误； C.∠1与∠2不是对顶角，故本选项错误； D.∠1与∠2是对顶角，故本选项正确； 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.3 多项式与多项式相乘 同步练习 题型：解答题

    如图,小思同学用A,B,C三类卡片若干张拼出了一个长为2a+b,宽为a+b的长方形图形.请你通过计算求出小思同学拼这个长方形所用A,B,C三类卡片各几张(要求:所拼图形中,卡片之间不能重叠,不能有空隙),并画出他的拼图示意图.

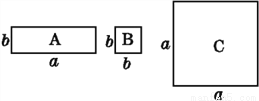
    A卡片3张，B卡片1张，C卡片2张. 【解析】试题分析：根据长方形的面积公式求出拼接后的长方形的面积，再利用多项式的乘法运算法则进行计算，然后根据系数即可得解． 试题解析：【解析】 根据题意得：（2a+b）（a+b）=2a2+2ab+ab+b2=2a2+3ab+b2； ∵A、B、C三类卡片的面积分别为ab、b2、a2， ∴所以A、B、C三类卡片分别为3张，1张，2张； ...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.2 单项式与多项式相乘 同步练习 题型：解答题

    当m,n为何值时, 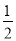x[x(x+m)+nx(x+1)+m] 的展开式中不含x2项和x3项?

    m=1,n=-1. 【解析】试题分析：原式去括号得到最简结果，根据结果中不含x2和x3的项，求出m与n的值即可． 试题解析：【解析】 x[x(x+m)+nx(x+1)+m]= x(x2+mx+nx2+nx+m)= (1+n)x3+ (m+n)x2+mx． 因为展开式中不含x2项和x3项，所以1+n=0，m+n=0，解得n=－1，m=1．

    查看答案和解析>>

    同步练习册答案