
如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
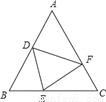
A. 75° B. 70° C. 65° D. 60°
C 【解析】试题分析:因为AB=AC,∠A=50°,所以∠B=∠C=65°,又因为BD=CE,BE=CF,所以ΔBDE≌ΔCEF,所以∠BED=∠CFE,因为∠CFE+∠CEF=180°-65°=115°,所以∠BED+∠CEF=115°,所以∠DEF=180°-(∠BED+∠CEF)=180°-115°=65°,故选:C.科目:初中数学 来源:2017年江苏省徐州市中考数学模拟试卷(2) 题型:单选题
下列几何体中,同一个几何体的主视图与俯视图不同的是( )
A. 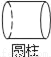 B.
B. 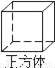 C.
C. 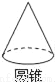 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(十) 题型:填空题
如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长为1cm,则这个圆锥的底面半径为_____.
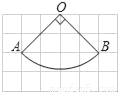
查看答案和解析>>
科目:初中数学 来源:安徽省淮南市潘集区2017-2018学年八年级上学期第二次联考数学试卷 题型:解答题
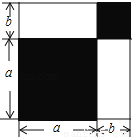
请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);并由此得到怎样的等量关系?请用等式表示;
(2)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值; ②a-b的值.
查看答案和解析>>
科目:初中数学 来源:安徽省淮南市潘集区2017-2018学年八年级上学期第二次联考数学试卷 题型:填空题
在平面直角坐标系xOy中,已知点A(2,3),在坐标轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有______个.
8 【解析】试题分析:在x轴的正半轴和y轴的正半轴上各有2个,在x轴的负半轴和y轴的负半轴上各有1个,总计有6个.查看答案和解析>>
科目:初中数学 来源:安徽省淮南市潘集区2017-2018学年八年级上学期第二次联考数学试卷 题型:单选题
如图,已知∠ADB=∠CBD,下列所给条件不能证明△ABD≌△CDB的是( )
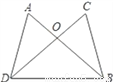
A. ∠A=∠C B. AD=BC C. ∠ABD=∠CDB D. AB=CD
D 【解析】A. ∵∠A=∠C ,∠ADB=∠CBD,BD=BD, ∴△ABD≌△CDB(AAS),故正确; B. ∵AD=BC ,∠ADB=∠CBD, BD=DB, ∴△ABD≌△CDB(SAS),故正确; C. ∵∠ABD=∠CDB , ∠ADB=∠CBD,BD=DB, ∴△ABD≌△CDB(ASA),故正确; D. ∵ AB=CD,BD=DB,∠ADB=∠CBD,不符...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上期末模拟数学试卷 题型:解答题
要加工200个零件,甲先单独加工了5小时,然后又与乙一起加工了4小时完成了任务.已知甲每小时比乙多加工2个零件,问甲、乙二人每小时各加工多少个零件?
甲每小时加工16个零件,乙每小时加工14个零件. 【解析】试题分析:如果乙每小时加工x个零件,那么甲每小时加工(x+2)个零件,根据要加工200个零件,甲先单独加工5小时,然后又与乙一起加工4小时,完成了任务以及甲每小时比乙多加工2个,可列出方程求解即可. 试题解析:【解析】 设乙每小时加工x个零件,那么甲每小时加工(x+2)个零件.根据题意,列方程,得: 5(x+2)+4(x...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级上期末模拟数学试卷 题型:单选题
在一次数学实践探究活动中,大家遇到了这样的问题:
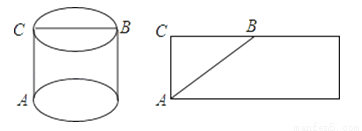
如图,在一个圆柱体形状的包装盒的底部A处有一只壁虎,在顶部B处有一只小昆虫,壁虎沿着什么路线爬行,才能以最短的路线接近小昆虫?
楠楠同学设计的方案是壁虎沿着A﹣C﹣B爬行;
浩浩同学设计的方案是将包装盒展开,在侧面展开图上连接AB,然后壁虎在包装盒的表面上沿着AB爬行.
在这两位同学的设计中,哪位同学的设计是最短路线呢?他们的理论依据是什么?( )
A. 楠楠同学正确,他的理论依据是“直线段最短”
B. 浩浩同学正确,他的理论依据是“两点确定一条直线”
C. 楠楠同学正确,他的理论依据是“垂线段最短”
D. 浩浩同学正确,他的理论依据是“两点之间,线段最短”
D 【解析】【解析】 由题意可得:浩浩同学正确,他的理论依据是“两点之间,线段最短”.故选D.查看答案和解析>>
科目:初中数学 来源:甘肃省张掖市高台县2016-2017学年八年级(上)期末数学试卷 题型:填空题
当m=______时,函数y=(2m﹣1)x3m﹣2是正比例函数.
1. 【解析】试题解析:函数y=(2m﹣1)x3m﹣2是正比例函数. 解得: 故答案为:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com