
下列图形中,既是轴对称图形又是中心对称图形的是 ( )
A.  B.
B.  C.
C.  D.
D. 
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:解答题
点 的坐标为
的坐标为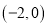 ,点
,点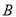 的坐标为
的坐标为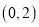 ,点
,点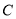 的坐标为
的坐标为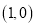 .
.
(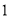 )在
)在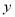 轴上是否存在点
轴上是否存在点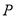 ,使
,使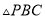 为等腰三角形,求出点
为等腰三角形,求出点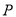 坐标.
坐标.
(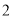 )在
)在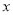 轴上方存在点
轴上方存在点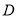 ,使以点
,使以点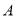 ,
, 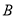 ,
, 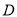 为顶点的三角形与
为顶点的三角形与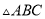 全等,画出
全等,画出 并请直接写出点
并请直接写出点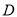 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
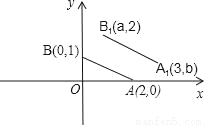
如图,A,B的坐标为(2,0),(0,1)若将线段AB平移至A1B1,则a+b的值为_____.
查看答案和解析>>
科目:初中数学 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:填空题
一元二次方程a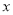 2+b
2+b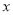 +c=0的两根是-
+c=0的两根是-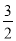 、-1,则二次函数y=a
、-1,则二次函数y=a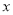 2+b
2+b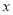 +c的图象与
+c的图象与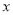 轴的两个交点间的距离为 .
轴的两个交点间的距离为 .
查看答案和解析>>
科目:初中数学 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
把抛物线y=(x+2)2向下平移2各单位长度,再向右平移2个单位长度,所得抛物线的解析式为 ( )
A. y=( 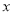 +2)2+2 B. y=2(
+2)2+2 B. y=2(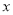 -1)2+4
-1)2+4
C. y= 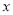 2+2 D. y=
2+2 D. y= 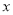 2-2
2-2
查看答案和解析>>
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(一) 题型:填空题
若三角形的边长分别为6、8、10,则它的最长边上的高为_____.
4.8 【解析】∵三角形三边的长分别为6、8和10,62+82=100=102, ∴此三角形是直角三角形,边长为10的边是最大边,设它的最大边上的高是h, ∴6×8=10h,解得,h=4.8, 故答案为:4.8.查看答案和解析>>
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(一) 题型:单选题
已知矩形的面积为10,长和宽分别为x和y,则y关于x的函数图象大致是( )
A. 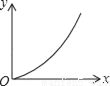 B.
B. 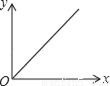 C.
C. 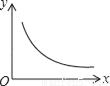 D.
D. 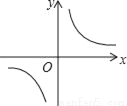
查看答案和解析>>
科目:初中数学 来源:江苏省徐州市区联校2017-2018学年八年级上学期期中联考数学试卷 题型:填空题
如图,已知所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5,则A,B,C,D四个小正方形的面积之和等于________ .
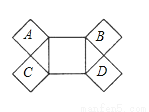
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
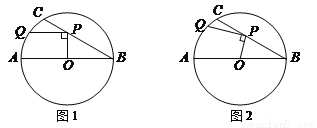
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
(1);(2). 【解析】试题分析:(1)在Rt△OPB中,由OP=OB·tan∠ABC可求得OP=,连接OQ,在Rt△OPQ中,根据勾股定理可得PQ的长;(2)由勾股定理可知OQ为定值,所以当当OP最小时,PQ最大.根据垂线段最短可知,当OP⊥BC时OP最小,所以在Rt△OPB中,由OP=OB·sin∠ABC求得OP的长;在Rt△OPQ中,根据勾股定理求得PQ的长. 试题解析:【解析...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com