练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    方程x2+x-12=0的两个根为（　　）

    A. x1=-2，x2=6 B. x1=-6，x2=2 C. x1=-3，x2=4 D. x1=-4，x2=3

    D 【解析】试题分析：将x2+x﹣12分解因式成（x+4）（x﹣3），解x+4=0或x﹣3=0即可得出结论． x2+x﹣12=（x+4）（x﹣3）=0， 则x+4=0，或x﹣3=0， 解得：x1=﹣4，x2=3．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型：解答题

    公式法求一元二次方程x2-3x-2=0的解

    【解析】试题分析：找出a、b、c的值，代入求根公式即可． 试题解析：【解析】 ∵a=1，b=-3，c=-2；∴b2-4ac =（-3）2-4×1×（-2）=9+8=17，∴x=．

    查看答案和解析>>

    科目：初中数学 来源：北师大版数学九年级上册第一章特殊平行四边形第二节《矩形的性质与判定》课时练习 题型：单选题

    如图，矩形ABCD的两条对角线交于点O，若∠AOD=120°，AB=6，则AC等于（ ）

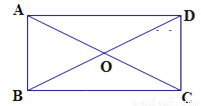
    A. 8 B. 10 C. 12 D. 18

    C 【解析】试题分析：根据∠AOD=120°可得∠AOB=60°，根据矩形的性质可得AO=BO，则△AOB是正三角形，则AO=AB=6，则AC=2AO=12．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级数学（上）第二章《一元二次方程》同步测试：2.4用因式分解法求解一元二次方程 题型：填空题

    方程（x-3）2=x-3的根是_________________．

    x1=3，x2=4 【解析】【解析】 （x﹣3）2=x﹣3，（x﹣3）2﹣（x﹣3）=0，（x﹣3）（x﹣3﹣1）=0，∴x1=3，x2=4．故答案为：x1=3，x2=4．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级数学（上）第二章《一元二次方程》同步测试：2.4用因式分解法求解一元二次方程 题型：单选题

    根据图中的程序，当输入方程x2=2x的解x时，输出结果y=（　　）

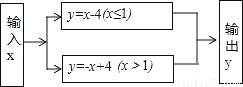
    A. -4 B. 2 C. -4或2 D. 2或-2

    C 【解析】【解析】 x2=2x，x2﹣2x=0，x（x﹣2）=0，∴x=0或x=2． 当x=0时，y=x﹣4=0﹣4=﹣4； 当x=2时，y=﹣x+4=﹣2+4=2．故选C．

    查看答案和解析>>

    科目：初中数学 来源：初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型：填空题

    如图，在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，将△ABE沿AE所在直线翻折得△AB1E，则△AB1E与四边形AECD重叠部分的面积是_______．

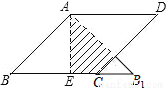
    【解析】【解析】 如图，设CD与AB1交于点O，∵在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，∴AE=，由折叠易得△ABB1为等腰直角三角形，∴S△ABB1=BA•AB1=2，S△ABE=1，∴CB1=2BE﹣BC=，∵AB∥CD，∴∠OCB1=∠B=45°，又由折叠的性质知，∠B1=∠B=45°，∴CO=OB1=，∴S△COB1=OC•OB1=，∴重叠部分的面积为：2﹣1﹣（...

    查看答案和解析>>

    科目：初中数学 来源：初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型：单选题

    菱形ABCD的周长是20，对角线AC=8，则菱形ABCD的面积是（　　）

    A. 12 B. 24 C. 40 D. 48

    B 【解析】【解析】 ∵菱形ABCD的周长是20，∴AB=20÷4=5，AC⊥BD，OA=AC=4，∴OB= =3，∴BD=2OB=6，∴菱形ABCD的面积是： AC•BD=×8×6=24．故选B．

    查看答案和解析>>

    科目：初中数学 来源：广西柳州市2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    若一个角是34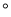，则这个角的余角是_______.

    56 【解析】【解析】 这个角的余角=90°－34°=56°．故答案为：56．

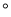    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型：解答题

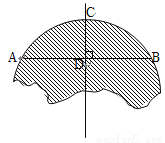
    如图，破残的圆形轮片上，弦AB的垂直平分线交弧AB于点C，交弦AB于点D.已知：AB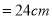, CD.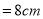

    (1)求作此残片所在的圆（不写作法，保留作图痕迹）；

    (2)求（1）中所作圆的半径.

    （1）作图见解析；（2）13cm. 【解析】试题分析：（1）根据垂径定理，即可求得圆心； （2）连接OA，根据垂径定理与勾股定理，即可求得圆的半径长． 试题解析：（1）连接BC，作线段BC的垂直平分线交直线CD与点O， 以点O为圆心，OA长为半径画圆， 圆O即为所求； （2）如图，连接OA， ∵OD⊥AB，AB， ∴AD=AB=12cm， 设圆...

    查看答案和解析>>

    同步练习册答案