练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    当行驶中的汽车撞到物体时，汽车的损坏程度通常用“撞击影响”来衡量．汽车的撞击影响I可以用汽车行驶速度v(km/min)来表示，下表是某种型号汽车的行驶速度与撞击影响的试验数据：

    v(km/min)

    0

    1

    2

    3

    4

    I

    0

    2

    8

    18

    32

    (1)请根据上表中的数据，在直角坐标系中描出坐标(v，I)所对应的点，并用光滑曲线将各点连接起来；

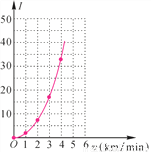
    (2)填写下表，并根据表中数据的呈现规律，猜想用v表示I的二次函数表达式；

    v(km/min)

    1

    2

    3

    4

    (3)当汽车的速度分别是1.5 km/min，2.5 km/min，4.5 km/min时，利用你得到的撞击影响公式，计算撞击影响分别是多少？

    【解析】 (1)如图所示；(2)2v2；(3)4.5，12.5，40.5. 【解析】试题分析：将表（1）里各个数据在直角坐标系里描出，连接各点，形成的光滑曲线就是速度与撞击影响之间的函数图象.从表格里可看出速度与撞击影响的函数表达式为I=2v2;当V=1.5,2.5,4.5时，代入函数表达式中可求得撞击影响. 【解析】 (1)如图所示． (2)由表格得I＝2v2. (3...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教七年级下册数学第九章-不等式与不等式组单元测试 题型：填空题

    若不等式组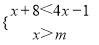的解集是x＞3，则m的取值范围是________．

    m≤3 【解析】解不等式x+8＜4x-1可得x＞3，然后根据不等式组的解集可知其公共部分为x＞3，所以可知m的取值范围为：m≤3. 故答案为：m≤3.

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：填空题

    如图是二次函数y＝a(x＋1)2＋2图象的一部分，该图象在y轴右侧与x轴交点的坐标是________．

    (1，0) 【解析】试题分析：根据函数表达式和函数图像可以看出二次函数的对称轴是x=-1，该图象在y轴左侧与x轴交点的坐标是（-3,0），所以该图象在y轴右侧与x轴交点的坐标与(-3,0) 关于对称轴对称，所以该图象在y轴右侧与x轴交点的坐标是（1,0）

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：单选题

    若抛物线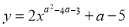的顶点在x轴下方，则( )

    A. a＝5 B. a＝5或a＝－1 C. a＝－1 D. a＝－5

    C 【解析】试题分析：y＝2xa2－4a－3＋a－5是抛物线。所以a2-4a-3=2,解得a=-1或a=5，已知抛物线顶点在x轴下方，所以a-5<0所以a<5,所以a=-1,故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：单选题

    抛物线y＝2x2－3的顶点在( )

    A. 第一象限 B. 第二象限 C. x轴上 D. y轴

    D 【解析】试题分析：b=0，抛物线的对称轴是y轴，所以顶点在y轴上，故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：解答题

    已知抛物线y＝ax2经过点(1，3)．

    (1)求a的值；

    (2)当x＝3时，求y的值；

    (3)说出此二次函数的三条性质．

    (1) 3；(2) 27；(3)答案不唯一， 【解析】试题分析：抛物线y＝ax2经过点(1，3)，将点代入即可求得a=3,将x=3代入函数中求得y=27.二次函数的性质可以通过从开口方向，对称轴，顶点坐标，增减性等方面进行分析. 【解析】 (1)∵抛物线y＝ax2经过点(1，3)， ∴a·1＝3.∴a＝3. (2)把x＝3代入抛物线y＝3x2，得y＝3×32＝27. ...

    查看答案和解析>>

    科目：初中数学 来源：2017年秋（北师大版）九年级数学下册（河南）检测：2.2　二次函数的图象与性质 题型：填空题

    下列各点：(-1，2)，(-1，-2)，(-2，-4)，(-2，4)，其中在二次函数y=-2x2的图象上的是____.

    (-1，-2). 【解析】试题分析：可将各点代入二次函数里，如果能使等式两边相等，即说明点在函数图象上.可得(－1，－2)在函数图象上.

    查看答案和解析>>

    科目：初中数学 来源：上海市浦东新区第四教育署2017-2018学年八年级（五四学制）上学期期中质量调研数学试卷 题型：填空题

    关于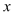的方程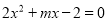的一个根是2 ，则_______ .

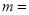    -3 【解析】试题解析：设方程的另一根为x2． ∵关于x的方程2x2+mx-2=0的一个根2， ∴x=2满足该方程， ∴2×22-2m-2=0， 解得：m=-3.

    查看答案和解析>>

    科目：初中数学 来源：黑龙江省大庆市（五四制）2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    观察下列等式：

    9-1=2×4，16-4=3×4，25-9=4×4，36-16=5×4，…，这些等式反映出自然数间的某种规律，设n表示自然数，请你猜想出这个规律，用含n的等式表示出来.并加以证明.

    (n+2)2-n2=4(n+1) 【解析】试题分析：先将等式进行整理，仔细观察分析整理后的等式不难发现存在的规律，用关于n的等式表示出来即可． 试题解析：将等式进行整理得： 32?12=4(1+1)； 42?22=4(2+1)； 52?32=4(3+1)； … 所以规律为：(n+2)2?n2=4(n+1). 证明：左边=n2+4n+4?n2=4n+4...

    查看答案和解析>>

    同步练习册答案