
��ͼ����ƽ��ֱ������ϵ�У� 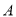 ��
�� 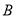 ���������ֱ�Ϊ
���������ֱ�Ϊ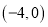 ��
�� 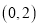 ������
������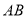 �����Ե�
�����Ե�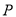 ��
�� 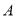 ��
�� 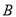 Ϊ������������ǵ���ֱ�������Σ����
Ϊ������������ǵ���ֱ�������Σ����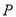 ����Ϊ__________��
����Ϊ__________��
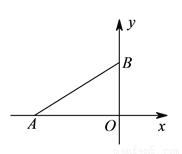

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ��������2017-2018ѧ����꼶��ѧ����ĩ���������ѧ�Ծ� ���ͣ������
��Rt��ABC�У�a��b��Ϊֱ�DZ����䳤��Ϊ���ڵ�������������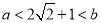 ��
��
���ֱ��������б���ϵĸߵij���Ϊ__________��
����������������� ����������ֱ�DZ�Ϊ3��4�� �����ε�б�� �������ֱ��������б���ϵĸߵij��� �ʴ�Ϊ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡʮ���е�������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��ͼ��A��P��B��C�ǰ뾶Ϊ8�ġ�O�ϵ��ĵ㣬�������BAC=��APC=60�㣬
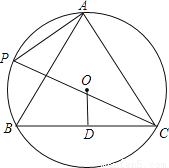
��1����֤����ABC�ǵȱ������Σ�
��2����Բ��O��BC�ľ���OD��
��1��֤����������2��4 ���������������� ��1��֤�����ߡ�APC�͡�ABC��ͬ�����Ե�Բ�ܽǣ����APC=��ABC�� �֡��ڡ�ABC�У���BAC=��APC=60�㣬���ABC=60�㡣 ���ACB=180�㩁��BAC����ABC=180�㩁60�㩁60��=60�㡣 ���ABC�ǵȱ������Ρ� ��2������OB�� �ߡ�ABCΪ�ȱ������Σ���OΪ�����Բ�� ��O...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡʮ���е�������2018����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����A��B��C�ڡ�O�ϣ�AC��OB����BAO=25�㣬���BOC�Ķ���Ϊ�� ��
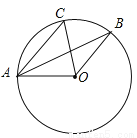
A. 25�� B. 50�� C. 60�� D. 80��
B ������������������ȸ���OA=OB����BAO=25��ó���B=25�㣬����ƽ���ߵ����ʵó���B=��CAB=25�㣬����Բ�ܽǶ������ɵó����ۣ� ��OA=OB����BAO=25�㣬���B=25�㣮 ��AC��OB�����B=��CAB=25�㣬���BOC=2��CAB=50�㣮��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����а�����2017-2018ѧ����꼶��ѧ��������ѧ�Ծ����������� ���ͣ������
��ͼ��  ��
��  ƽ��
ƽ�� ��
�� 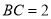 ��
�� 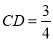 ����
����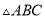 �������
�������
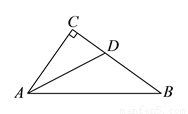
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����а�����2017-2018ѧ����꼶��ѧ��������ѧ�Ծ����������� ���ͣ���ѡ��
��֪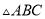 �У�
�� 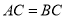 ��
�� 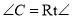 ����ͼ����
����ͼ����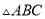 �����۵���ʹ��
�����۵���ʹ��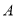 �����߶�
�����߶�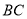 �ϣ�������
�ϣ�������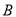 �͵�
�͵�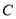 �������
�������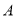 �����Ϊ
�����Ϊ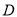 ���ۺ�Ϊ
���ۺ�Ϊ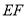 ����
����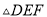 �ǵ���������ʱ����
�ǵ���������ʱ����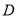 ���ܵ�λ�ù��У� ����
���ܵ�λ�ù��У� ����

A. 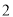 �� B.
�� B. 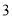 �� C.
�� C. 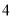 �� D.
�� D. 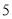 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭ʡ�����а�����2017-2018ѧ����꼶��ѧ��������ѧ�Ծ����������� ���ͣ���ѡ��
��֪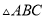 �У�
�У� 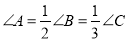 ��������������֮��Ϊ�� ����
��������������֮��Ϊ�� ����
A. 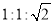 B.
B. 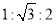 C.
C. 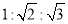 D.
D. 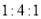
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㶫ʡ�����з�خ��2017-2018ѧ����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
2013�꣬�ҹ��Ϻ��Ͱ������ȷ��֡�H7N9�����������в������˲��������ʶ���Σ��������β��������ֱ��Ϊ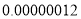 �ף���һֱ���ÿ�ѧ��������ʾΪ____�ף�
�ף���һֱ���ÿ�ѧ��������ʾΪ____�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�γ���2017����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ��AB�ǡ�O��ֱ����CΪ��O��һ�㣬AD��CD������D�ڡ�O�⣩ACƽ�֡�BAD��
��1����֤��CD�ǡ�O�����ߣ�
��2����DC��AB���ӳ����ཻ�ڵ�E����DE��12��AD��9����BE�ij���
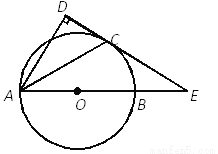
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com