
Ϊ�����÷���H1N1�������й������������������Ӽס��ҡ�����λҽ����A��B������ʿ��ѡȡһλҽ����һ����ʿָ��ij����Ԥ��H1N1�������й�����
��1�������ѡһλҽ����һ����ʿ������״ͼ�����б�������ʾ���п��ܳ��ֵĽ����
��2����ǡ��ѡ��ҽ���ͻ�ʿA�ĸ��ʣ�
��1����״ͼ��������2�� ���������������������״ͼ���оٳ�ҽ�����ܵ��������3����ʿ���ܵ��������2�������������ǡ��ѡ��ҽ���ͻ�ʿA�������ռ����������Ķ��ټ��ɣ� �����������1�����б�����ʾ���п��ܽ�����£� ��2��P��ǡ��ѡ��ҽ���ͻ�ʿA�� ��ǡ��ѡ��ҽ���ͻ�ʿA�ĸ�����
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㶫ʡ�����н�������У2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
������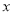 ��һԪ���η���
��һԪ���η���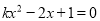 ����������ȵ�ʵ��������
����������ȵ�ʵ��������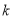 ��ȡֵ��ΧΪ________
��ȡֵ��ΧΪ________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������˳����2018�������ѧ����ĩ������ѧ�Ծ� ���ͣ������
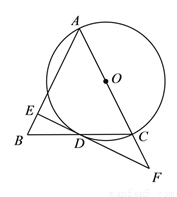
��֪����ͼ���ڡ�ABC�У�AB=AC����ACΪֱ������O��BC�ڵ�D������D����O�����߽�AB�ڵ�E����AC���ӳ����ڵ�F��
��1����֤��DE��AB��
��2����tan��BDE=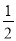 , CF=3����DF�ij���
, CF=3����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������˳����2018�������ѧ����ĩ������ѧ�Ծ� ���ͣ������
�ֽ���ʽ��a2b��2ab+b=_______��
b��a��1��2 ������������ȡ����ʽb����������ȫƽ����ʽ���ж��ηֽ⣮ �������� a2b��2ab+b�� =b��a2��2a+1��������ȡ����ʽ�� =b��a��1��2������ȫƽ����ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������˳����2018�������ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ͼ���ڡ�ABC�У���A=90�㣮��AB=12��AC=5����cosC��ֵΪ�� ��

A. 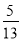 B.
B. 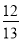 C.
C. 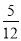 D.
D. 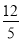
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���������о��꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ������
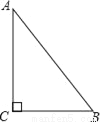
��Rt��ABC�У���C=90�㣮
��1���ó߹���ͼ��Rt��ABC������P����������ͼ�ۼ�����Ҫ��д������֤������
��2������ΪֻҪ֪��Rt��ABC��һ���ߵij����������������������֮��ľ��룿������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���������о��꼶���ϣ���ĩ��ѧ�Ծ� ���ͣ������
�ֽ���ʽ��3x2��6x2y+3xy2=_____��
3x��x��2xy+y2�� �����������������ԭʽ �ʴ�Ϊ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2017-2018ѧ���һѧ�ڰ��꼶��ѧ�����Ծ� ���ͣ������
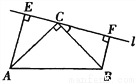
��ͼ���ڡ�ABC�У���ACB��90�㣬AC��BC��ֱ��l��������C����A��B����ֱ���l�Ĵ���AE��BF��E��FΪ���㣮��ֱ��l����ױ�AB�ཻʱ��
��֤��EF��AE��BF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������з�У2017-2018ѧ��ȵ�һѧ�����г�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ�����������ĸ�������AB=DE��BC=EF����B=��E����C=��F��������ѡ����������ʹ��ABC�ա�DEF�Ĺ��У�������
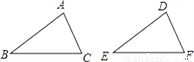
A. 1�� B. 2�� C. 3�� D. 4��
C ���������������ĸ������У���ѡ������������4�ֲ�ͬ����ϣ� ��1����AB=DE����B=��E��BC=EF�ɸ��ݡ�SAS��֤�ã���ABC�ա�DEF����2���ɡ�B=��E����C=��F��AB=DE�ɸ��ݡ�AAS�� ֤�ã���ABC�ա�DEF����3���ɡ�B=��E��BC=EF����C=��F�ɸ��ݡ�ASA��֤�ã���ABC�ա�DEF����4����AB=DE��BC=EF����C=��F����֤����ABC���DEFȫ...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com