
ij��������ÿ��50Ԫ�ļ۸�800��T������һ�����Ե���80Ԫ���ۣ��۳���200�����ڶ�����������۲��䣬Ԥ���Կ��۳�200����������Ϊ�����������������������ۣ������г����飬����ÿ����1Ԫ���ɶ��۳�10��������͵���Ӧ���ڹ����ļ۸ڶ����½����������̽���ʣ���T��һ����������ۣ����ʱ����Ϊ40Ԫ����ڶ����µ��۽���xԪ��
��1������������軯��
ʱ�� | ��һ���� | �ڶ����� | ���ʱ |
���ۣ�Ԫ�� | 80 |
| 40 |
������������ | 200 |
|
|
��2�����������ϣ��ͨ����������T������9000Ԫ����ô�ڶ����µĵ���Ӧ�Ƕ���Ԫ��
��1���ڶ����µĵ���Ϊ��80-x������Ϊ��200+10x�����Ϊ��800-200-��200+10x������2��70. ����������������� ��1��80��x��200+10x��800��200�� ʱ�� ��һ���� �ڶ����� ���ʱ ���ۣ�Ԫ�� 80 80��x 40 ������������ 200 ...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������� 2017-2018ѧ�� ���꼶��ѧ�ϲ� һԪ���η��� ��ʽ�ֽⷨ ר����ϰ�����𰸣� ���ͣ������
һԪ���η���x(x+3)=x�Ľ���______��
x1=0��x2=��2�� ��������������������÷ֽ���ʽ��������⣮ x��x+3��=0����x=0��x=��3�� �ʴ�Ϊ��x=0��x=��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧģ���Ծ� ���ͣ������
��ͼ����������ABCD����һ��P����AP=AB��PB=PC������AC��PD��
��֤����1����APB�ա�DPC����2����BAP=2��PAC��
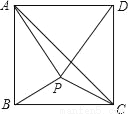
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
һ�������ĸ�ľ�����������V=4m3ʱ�������ܶȦ�=0.25��103 kg/m3�������V�ĺ�����ϵʽ�ǣ�������
A. ��=1000V B. ��=V+1 000 C. ��=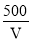 D. ��=
D. ��=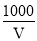
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
������x�ķ���x2+2x+a=0������ʵ��������a��ȡֵ��Χ�ǣ�������
A. a��1 B. a��1 C. a��1 D. a��1
B �������������������=4-4a��0����a��1�� ��ѡ��B�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����ѧ�������г�����ѧ��ĩ�ۺϼ�� ���ͣ������
��֪����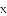
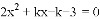 .
.
(1)��֤:��������������ȵ�ʵ����;
(2)�������һ��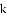
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����ѧ�������г�����ѧ��ĩ�ۺϼ�� ���ͣ������
��ͼ����A��B��C�ڡ�O�ϣ�����BAC = 24�㣬���OBC = �㣮
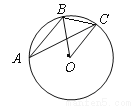
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�ij���ݷ��2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
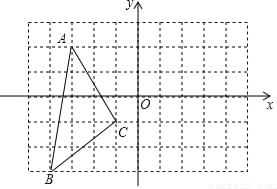
��ͼ��
��1��������ABC����y��ĶԳ�ͼ�Ρ�A1B1C1��
��2��ֱ��д����ABC����x��ԳƵ������Ρ�A2B2C2�ĸ������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹŶ�����˹��2017-2018ѧ���һѧ�������Ծ���һ��ѧ. ���ͣ������
��֪����ĸa.b�Ķ���ʽ��:3[a2+2(ab��3)]-3a2.4(ab��a��2)
��1���������ʽ;
��2����a.b��Ϊ��������a.b���뻯��Ķ���ʽ�У�ǡ�û���Ķ���ʽ��ֵ����0������ĸa��ֵ;
��3��ͬѧС���ӻ���Ķ���ʽ�з��֣�ֻҪ��ĸbȡһ���̶�������������ĸaȡ����������ʽ��ֵ��Ϊһ�������������ôС����ȡ����ĸb��ֵ�Ƕ�����?
��1��ԭʽ=-10ab+4a-10����2��ԭʽ=-10+4a-10=10��a=5����3��b= ���������������: ��1��ԭʽȥ���źϲ����ɵõ������ ��2����a��b��Ϊ�����õ�ab=1�����루1������м������b��ֵ���ɣ� ��3�����ݣ�1���Ľ��ȷ����b��ֵ���ɣ� �������: (1���������� ԭʽ=3(a2-2ab-6)-3a2-4(ab-a-2) =3a2-...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com