
据统计,全球每分钟约有8500000吨污水排入江河湖海,则8500000用科学记数法表示为________.
8.5×106 【解析】根据科学记数法的表现形式可得: 8500000用科学记数法表示为,故答案为: . 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
下列计算正确的是( )
A. 2a+3b=5ab B. 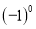 =l C.
=l C. 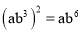 D.
D. 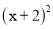
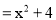
查看答案和解析>>
科目:初中数学 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:填空题
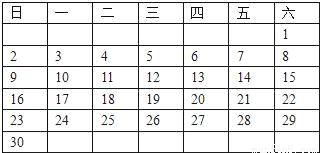
如图是2003年11月份的日历,现用一矩形在日历中任意框出4个数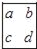 ,请用一个等式表示,a、b、c、d之间的关系_____.
,请用一个等式表示,a、b、c、d之间的关系_____.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:解答题
如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.
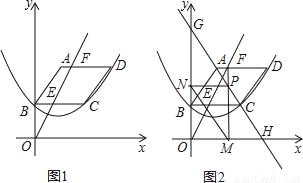
(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
(1)抛物线解析式为y=x2﹣x+3;(2)S=m﹣3(2<m≤6);(3)当m=时,MN最小=. 【解析】试题分析:(1)根据平行四边形的性质和抛物线的特点确定出点D,然而用待定系数法确定出抛物线的解析式.(2)根据AD∥BC∥x轴,且AD,BC间的距离为3,BC,x轴的距离也为3,F(m,6),确定出E(,3),从而求出梯形的面积.(3)先求出直线AC解析式,然后根据FM⊥x轴,表示出点...查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:解答题
解方程:y(y﹣4)=﹣1﹣2y.
【解析】试题分析:因式分解法. 试题解析: 整理得: 解得: 原方程的解是:查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:单选题
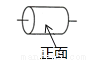
如图是一个水平放置的圆柱形物体,中间有一细棒,则此几何体的俯视图是( )
A. 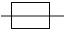 B.
B. 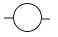 C.
C. 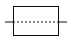 D.
D. 
查看答案和解析>>
科目:初中数学 来源:江西省2017年秋人教七年级数学上册期末模拟卷 题型:单选题
如图中的图像(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减小.⑤汽车离出发地64千米是在汽车出发后1.2小时时。其中正确的说法共有( )
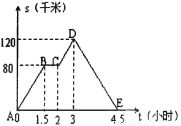
A.1个 B.2个 C.3个 D.4个
A. 【解析】 试题分析:根据图象对每条进行分别判断即可,行驶的最远距离是120千米,共行驶240千米,共用时间是4.5小时. ①行驶的最远距离是120千米,共行驶240千米,故此选项错误; ②根据图象从1.5时到2时,是停留时间,停留0.5小时,故此选项正确; ③汽车在整个行驶过程中的平均速度为千米/时,故此选项错误; ④汽车自出发后3小时至4.5小时之间路程...查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年九年级第一学期第一次月考数学试卷 题型:解答题
已知关于x的一元二次方程x2﹣2mx+(m﹣1)2=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=28时,求m的值.
(1)m≥;(2)符合条件的m的值为3. 【解析】试题分析:(1)若一元二次方程有两个等实数根,则根的判别式△=b2-4ac≥0,建立关于m的不等式,即可求出m的取值范围; (2)根据根与系数的关系,可得x1+x2=2m,x1·x2=(m﹣1)2,再根据x12+x22=(x1+x2)2-2x1·x2即可求得m的值,结合(1)即可确定出m的具体值. 试题解析:(1)∵原方程有两个实...查看答案和解析>>
科目:初中数学 来源:山东省潍坊高新技术产业开发区2017-2018学年八年级上期末模拟数学试卷 题型:填空题
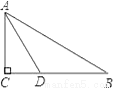
如图,△ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com