
如图是2003年11月份的日历,现用一矩形在日历中任意框出4个数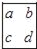 ,请用一个等式表示,a、b、c、d之间的关系_____.
,请用一个等式表示,a、b、c、d之间的关系_____.
科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:单选题
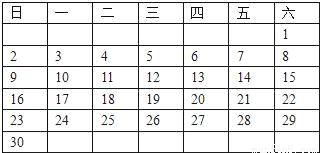
图中的平面展开图是下面名称几何体的展开图,则立体图形与平面展开图不相符的是( )
A.  三棱锥 B.
三棱锥 B.  长方体
长方体
C. 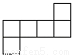 正方体 D.
正方体 D. 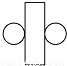 圆柱体
圆柱体
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:填空题
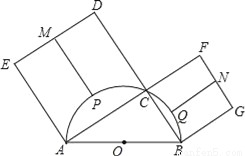
如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE,BCFG,DE,FG, 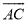 ,
, 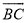 的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=18,则AB的长是_____.
的中点分别是M,N,P,Q.若MP+NQ=14,AC+BC=18,则AB的长是_____.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:单选题
下列方程中有实数根的是( )
A. x2+2x+2=0 B. x2﹣2x+3=0 C. x2﹣3x+1=0 D. x2+3x+4=0
C 【解析】解:A.△=22﹣4×1×2=﹣6<0,则该方程无实数根,故本选项错误; B.△=(﹣2)2﹣4×1×3=﹣8<0,则该方程无实数根,故本选项错误; C.△=(﹣3)2﹣4×1×1=5>0,则该方程有实数根,故本选项正确; D.△=32﹣4×1×4=﹣7<0,则该方程无实数根,故本选项错误; 故选C.查看答案和解析>>
科目:初中数学 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:解答题
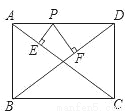
如图所示,在菱形ABCD中,点E,F分别在CD,BC上,且CE=CF,求证:AE=AF.
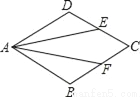
查看答案和解析>>
科目:初中数学 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:单选题
在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE⊥AC于E,PF⊥BD于F,则PE+PF的值为( )
A. 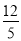 B. 2 C.
B. 2 C. 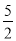 D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:单选题
如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为( )
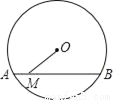
A. 2 B. 3 C. 4 D. 5
B 【解析】试题分析:根据垂线段最短可知,当时,线段OM的值最小 此时,连接OA,由垂径定理可知, 在查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:填空题
据统计,全球每分钟约有8500000吨污水排入江河湖海,则8500000用科学记数法表示为________.
8.5×106 【解析】根据科学记数法的表现形式可得: 8500000用科学记数法表示为,故答案为: .查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年九年级第一学期第一次月考数学试卷 题型:单选题
在某校“我的中国梦”演讲比赛中,有7名学生参加决赛,他们决赛的最终成绩各不相同,其中一名学生想要知道自己能否进入前3名,他不仅要了解自己的成绩,还要了解这7名学生成绩的( )
A. 众数 B. 方差 C. 平均数 D. 中位数
D 【解析】试题分析:由于其中一名学生想要知道自己能否进入前3名,共有7名选手参加,故应根据中位数的意义分析. 【解析】 因为7名学生进入前3名肯定是7名学生中最高成绩的3名, 而且7个不同的分数按从小到大排序后,中位数之后的共有3个数, 故只要知道自己的成绩和中位数就可以知道是否进入前3名. 故选:D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com