
��֪����ͼ����ƽ��ֱ������ϵxOy�У�����������y=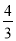 x��ͼ����A����A��������Ϊ4������������y=
x��ͼ����A����A��������Ϊ4������������y=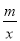 ��ͼ��Ҳ������A����һ�����ڵĵ�B�����������������ͼ���ϣ�����B��BC��x�ᣬ��y���ڵ�C����AC=AB����
��ͼ��Ҳ������A����һ�����ڵĵ�B�����������������ͼ���ϣ�����B��BC��x�ᣬ��y���ڵ�C����AC=AB����
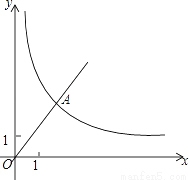
��1����������������Ľ���ʽ��
��2��ֱ��AB�ı���ʽ��
��1��y= ����2��y=��x+6�� �������������������1������������������ͼ���㣬���������Ϊ4�����������꣬���ݷ�����������ͼ���㣬�����ֵ�� ��2�����ݵ������͵��������ε��������������꣬���ô���ϵ�������ֱ�� �ı���ʽ�� ������� ������������ͼ���㣬���������Ϊ4�� ��������Ϊ��3��4���� �߷�����������ͼ���㣬 �෴���������Ľ���... �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ����������У2017-2018ѧ����꼶��ѧ������������ѧ�Ծ� ���ͣ������
���������ε��ܳ�Ϊ13 cm������һ�߳���3 cm����õ��������ε���Ϊ____cm��
5 �����������������������3cm�ı��ǵױ�ʱ������Ϊ3cm��5cm��5cm�����������γ����� ������3cm�ı�����ʱ���ױ߳��ǣ�13?3?3=7cm����3+3<7�������������ε����߹�ϵ. �������ǣ�5cm. �ʴ�Ϊ��5.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����б�Ӧ��2018����꼶��ѧ��12���¿���ѧ�Ծ� ���ͣ������
ij��Ʒ�Ľ���Ϊÿ��50Ԫ���ۼ�Ϊÿ��60Ԫ��ÿ�������190�������ÿ����Ʒ���ۼ�ÿ����1Ԫ����ÿ������10������ÿ����Ʒ���ۼ�����xԪ��xΪ����������ÿ�����������ΪyԪ��
��1����y����x�Ĺ�ϵʽ��
��2��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ�������ǡΪ1980Ԫ��
��3��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ��ɻ�����������������Ƕ���Ԫ��
��1��y=��10x2+90x+1900�� ��2��ÿ����Ʒ���ۼ۶�Ϊ61Ԫ��68Ԫʱ��ÿ�������ǡΪ1980Ԫ�� ��3��ÿ����Ʒ���ۼ۶�Ϊ64Ԫ��65Ԫʱ��ÿ��ɻ������������������2100Ԫ�� �������������������1��������������ÿ������=������ó���ϵʽ���ɣ� ��2�����ã�1���������ϵʽ������ʹy=1980�����ó����ɣ� ��3�������䷽��������κ�����ֵ�����...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����б�Ӧ��2018����꼶��ѧ��12���¿���ѧ�Ծ� ���ͣ���ѡ��
�ӱ�ʡ���ص������ŵ��Ź��ǽ��Ƶ��������Σ�������ͼ��ʾ��ƽ��ֱ������ϵ���亯���Ĺ�ϵʽΪ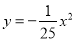 ����ˮ�����Ź����ĸ߶�DO��4mʱ����ʱˮ�����ABΪ��������
����ˮ�����Ź����ĸ߶�DO��4mʱ����ʱˮ�����ABΪ��������

A. ��20m B. ��10m C. 10m D. 20m
D ����������������B��������Ϊ?4�� ��y=?4���룬 ��x=��10�� ��A(?10,?4),B(10,?4)�� ��AB=20m. ��ˮ�����ABΪ20m. ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ̩����2017���п���ѧ��ģ�Ծ��������棩 ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��l��������y=mx2+nx�ཻ��A��1��3 ����B��4��0�����㣮
��1����������ߵĽ���ʽ��
��2�������������Ƿ���ڵ�D��ʹ�á�ABD�����߶�ABΪб�ߵ�ֱ�������Σ������ڣ������D�����ꣻ�������ڣ�˵�����ɣ�
��3����P���߶�AB��һ���㣬����P�����A��B�غϣ�������P��PM��OA������һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������BCN����PMN�����S��BCN��S��PMN����S��BCN=2S��PMN�����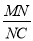 ��ֵ���������ʱ��M�����꣮
��ֵ���������ʱ��M�����꣮
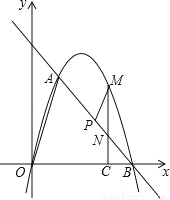
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ̩����2017���п���ѧ��ģ�Ծ��������棩 ���ͣ������
��ͼ���ھ���ABCD�У���E��F�ֱ���BC��CD�ϣ�����ABE��AE�۵���ʹ��B����AC�ϵĵ�B�䴦���ֽ���CEF��EF�۵���ʹ��C����EB����AD�Ľ���C�䴦����BC��AB��ֵΪ �� ��
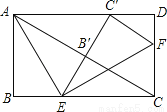
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ̩����2017���п���ѧ��ģ�Ծ��������棩 ���ͣ������
�ֽ���ʽ��a3��4a2+4a=_____��
a��a��2��2 ���������������������ȡ����ʽa����������ȫƽ����ʽ�ֽ⼴�ɣ� ���������ԭʽ=a��a2��4a+4��=a��a��2��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�п���ѧ��ģ�Ծ� ���ͣ������
��ͼ�������뾶��ȵ�ֱ�����ε�Բ�ķֱ��ڶԷ���Բ���ϣ��뾶AE��CF���ڵ�G���뾶BE��CD���ڵ�H���ҵ�C�� ���е㣬�����εİ뾶Ϊ2����ͼ����Ӱ���ֵ��������______��
���е㣬�����εİ뾶Ϊ2����ͼ����Ӱ���ֵ��������______��
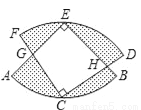
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���㽭�������������m��ʵ��ѧУ2018����꼶��ѧ�����п�����ѧ�Ծ����������� ���ͣ���ѡ��
�� ����һ��
����һ�� ������
������ ���������У����Ϊ
���������У����Ϊ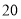 ����̵�Ϊ
����̵�Ϊ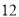 ����
����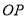 �ij��� ��
�ij��� ��
A. 6 B. 7 C. 8 D. 10
C �������������������ͼ�� AB��ֱ���� ����P��CD��AB����Բ�ڵ�C��D����. �ɴ�������֪����P��CD���е㣻 ��ѡC.�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com