练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一只不透明的袋子中装有4个黑球、2个白球，每个球除颜色外都相同，从中任意摸出3个球，下列事件为必然事件的是（ ）

    A. 至少有1个球是白球 B. 至少有1个球是黑球

    C. 至少有2个球是黑球 D. 至少有2个球是白球

    B 【解析】任意摸3个球，可能出现3黑、1白2黑、2白1黑，所以摸出至少一个黑球是必然事件. 故选B.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省2018届九年级12月月考数学试卷 题型：解答题

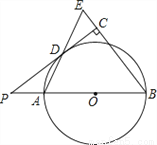
    如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE垂直于PD，交PD的延长线于点C，连接AD并延长，交BE于点E．

    （1）求证：AB=BE；

    （2）若PA=2，cosB=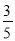，求⊙O半径的长．

    （1）证明见解析；（2）3. 【解析】试题分析：（1）连接OD，由PD切⊙O于点D，得到OD⊥PD，由于BE⊥PC，得到OD∥BE，得出∠ADO=∠E，根据等腰三角形的性质和等量代换可得结果； （2）由（1）知，OD∥BE，得到∠POD=∠B，根据三角函数的定义即可得到结果． 试题解析：（1）证明：连接OD， ∵PD切⊙O于点D， ∴OD⊥PD， ∵BE⊥PC，...

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市汉阳区2018届九年级（上）期中数学试卷（解析版） 题型：单选题

    某商品原价289元，经连续两次降价后售价为256元，设平均每降价的百分率为x，则下面所列方程正确的是（　　）

    A. 289（1﹣x）2=256 B. 256（1﹣x）2=289

    C. 289（1﹣2x）2=256 D. 256（1﹣2x）2=289

    A 【解析】由题意得289（1﹣x）2=256.所以选A.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016届九年级下学期二模数学试卷 题型：填空题

    点M是反比例函数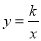 的图像上一点，MN垂直于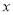轴，垂足是点N，若△MON的面积S△MON =2，则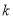的值为__________．

    k=±4 【解析】由题意得：S△OMN==2，解得k=±4. 故答案为±4.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016届九年级下学期二模数学试卷 题型：填空题

    埃是表示极小长度的单位名称，是为纪念瑞典物理学家埃基特朗而定的．1埃等于一亿分之一厘米，请用科学记数法表示1埃等于___________厘米．

    1×10-8 【解析】试题分析：此题考的是科学记数法： 由科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．因此1埃＝厘米.

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省海口市中考数学模拟试卷 题型：解答题

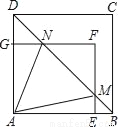
    如图，矩形AEFG的顶点E，G分别在正方形ABCD的AB，AD边上，连接B，交EF于点M，交FG于点N，设AE=a，AG=b，AB=c（b＜a＜c）．

    （1）求证： ；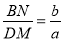

    （2）求△AMN的面积（用a，b，c的代数式表示）；

    （3）当∠MAN=45°时，求证：c2=2ab．

    （1）证明见解析；（2）c（a+b﹣c）；（3）证明见解析. 【解析】试题分析：（1）首先过点N作NH⊥AB于点H，过点M作MI⊥AD于点I，可得△NHB和△DIM是等腰直角三角形，四边形AGNH和四边形AEMI是矩形，则可求得BN=b，DM=a，继而求得答案； （2）由S△AMN=S△ABD-S△ABM-S△ADN，可得S△AMN=c2-c（c-a）-c（c-b），继而求得答案； ...

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省海口市中考数学模拟试卷 题型：填空题

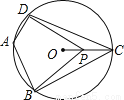
    如图，四边形ABCD内接于⊙O，∠DAB=120°，连接OC，点P是半径OC上任意一点，连接DP，BP，则∠BPD可能为______度（写出一个即可）．

    80 【解析】 连接OD、OB， ∵∠DAB=120°， ∴∠DCB=60°， ∴∠DOB=120°， ∴60°＜∠BPD＜120°， ∴∠BPD可能为80°. 故答案为80.

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省中考数学模拟试卷 题型：解答题

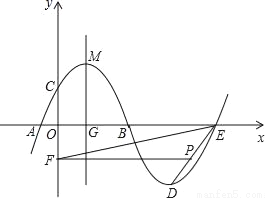
    如图，抛物线m：y=﹣0.25（x+h）2+k与x轴的交点为A，B，与y轴的交点为C，顶点为M（3，6.25），将抛物线m绕点B旋转180°，得到新的抛物线n，它的顶点为D．

    （1）求抛物线n的解析式；

    （2）设抛物线n与x轴的另一个交点为E，点P是线段DE上一个动点（P不与D，E重合），过点P作y轴的垂线，垂足为F，连接EF．如果P点的坐标为（x，y），△PEF的面积为S，求S与x的函数关系式，写出自变量x的取值范围，并求出S的最大值；

    （3）设抛物线m的对称轴与x轴的交点为G，以G为圆心，A，B两点间的距离为直径作⊙G，试判断直线CM与⊙G的位置关系，并说明理由．

    （1）y=x2﹣x+36；（2）S=﹣x2+x（13＜x＜18），△PEF的面积S没有最大值；（3）直线CM与⊙G相切，理由见解析. 【解析】试题分析：（1）根据抛物线m的顶点为M（3，6.25）得出m的解析式为y=-（x-3）2+=-（x-8）（x+2），求出A（-2，0），B（8，0），再根据旋转的性质得出D的坐标为（13，-6.25），进而求出抛物线n的解析式； （2）由点E与点A关...

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省中考数学模拟试卷 题型：单选题

    分式方程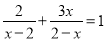的解为（　　）

    A. 1 B. 2 C. 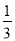D. 0

    A 【解析】试题分析：根据分式方程的解法：去分母，得2-3x=x-2，移项后解得x=1，检验x=1是原分式方程的根. 答案为A

    查看答案和解析>>

    同步练习册答案