练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

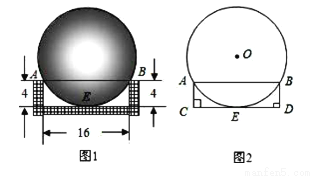
    用工件槽（如图1）可以检测一种铁球的大小是否符合要求，已知工件槽的两个底角均为90°，尺寸如图（单位：cm）．将形状规则的铁球放入槽内时，若同时具有图1所示的A、B、E三个接触点，该球的大小就符合要求．图2是过球心O及A、B、E三点的截面示意图，求这种铁球的直径．

    20㎝． 【解析】试题分析：连接OA、OE，设OE与AB交于点P，根据题意得出四边形ABCD为矩形，根据垂径定理得出PA=8cm，PE=4cm，然后根据Rt△AOP的勾股定理求出OA的值，从而得出圆的直径. 试题解析：连接OA、OE，设OE与AB交于点P，如图 ∵AC=BD，AC⊥CD，BD⊥CD ∴四边形ACDB是矩形 ∵CD=16cm，PE=4cm ∴PA=...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年内蒙古包头市七年级（下）期中数学试卷 题型：填空题

    如图，在△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于点D.给出下列结论：①∠EAB=∠FAC；②AF=AC；③∠C=∠EFA；④AD=AC.其中正确的结论是_____(填序号)．

    ①②③ 【解析】【解析】 在△AEF和△ABC中，∵AB=AE，∠B=∠E，BC=EF，∴△AEF≌△ABC（SAS），∴∠EAF=∠BAC，AF=AC，∠C=∠EFA，∴∠EAB=∠FAC，故①②③正确，④错误； 所以答案为：①②③．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古包头市八年级（下）期中数学试卷 题型：解答题

    某公司经营甲、乙两种商品，每件甲种商品进价12万元，售价14.5万元．每件乙种商品进价8 万元，售价10万元，且它们的进价和售价始终不变．现准备购进甲、乙两种商品共20件，所用 资金不低于190万元不高于200万元．

    （1）该公司有哪几种进货方案？

    （2）该公司采用哪种进货方案可获得最大利润？最大利润是多少？

    （1）有3种购买方案： 方案1：甲种商品购买8件，乙种商品购买12件， 方案2：甲种商品购买9件，乙种商品购买11件， 方案3：甲种商品购买10件，乙种商品购买10件， （2）采用第3种进货方案可获得最大利润，最大利润是45万元． 【解析】试题分析：（1）设购进甲商品x件，则购进乙商品（20﹣x）件，根据购买需要的资金不低于190万元不高于200万元建立不等式组，求出...

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古包头市八年级（下）期中数学试卷 题型：单选题

    如图，在△ABC中，∠C=90°，∠B=15°，AB的垂直平分线交BC于D，交AB于E，DB=12cm，则AC=（　　）

    A. 4cm B. 5m C. 6cm D. 7cm

    C 【解析】【解析】 连接AD．∵AB的垂直平分线交BC于D，交AB于E，DB=12cm，∴AD=BD=12cm，∠B=∠BAD=15°；又∵在△ABC中，∠C=90°，∠B=15°，∴∠DAC=60°，∴∠ADC=30°，∴AC=AD=6cm．故选C．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年内蒙古包头市八年级（下）期中数学试卷 题型：单选题

    下列不等式中，是一元一次不等式的是（　　）

    A. x+1＞2 B. x2＞9 C. 2x+y≤5 D. 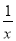＞3

    A 【解析】解：A．该不等式符合一元一次不等式的定义，故本选项正确； B．未知数的次数是2，不是一元一次不等式，故本选项错误； C．该不等式中含有2个未知数，属于二元一次不等式，故本选项错误； D．该不等式属于分式不等式，故本选项错误； 故选A．

    查看答案和解析>>

    科目：初中数学 来源：江西婺源县2016-2017学年第一学期期末考试九年级数学试卷 题型：填空题

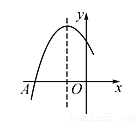
    如图是二次函数y＝ax2＋bx＋c图象的一部分，图象过点A（－3，0），对称轴为直线x＝－1，给出四个结论：①b2＞4ac；②2a＋b＝0；③a＋b＋c＞0；④若点B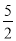（－，y1），C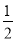（－，y2）为函数图象上的两点，则y1＜y2．其中正确结论是___________．

    ①④． 【解析】【解析】 由函数图象可知抛物线与x轴有2个交点，∴b2﹣4ac＞0即b2＞4ac，故①正确； ∵对称轴为直线x=﹣1，∴ =﹣1，即2a﹣b=0，故②错误； ∵抛物线与x轴的交点A坐标为（﹣3，0）且对称轴为x=﹣1，∴抛物线与x轴的另一交点为（1，0），∴将（1，0）代入解析式可得，a+b+c=0，故③错误； ∵a＜0，∴开口向下，∵|﹣+1|=，|﹣+...

    查看答案和解析>>

    科目：初中数学 来源：江西婺源县2016-2017学年第一学期期末考试九年级数学试卷 题型：单选题

    某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（　　）

    A. 560（1＋x）2＝315 B. 560（1－x）2＝315

    C. 560（1－2x）2＝315 D. 560（1－x2）＝315

    B 【解析】试题分析：根据题意，设设每次降价的百分率为x，可列方程为560（1-x）²=315. 故选：B

    查看答案和解析>>

    科目：初中数学 来源：江苏省连云港市灌南县2018届九年级上学期期中考试数学试卷 题型：解答题

    已知关于x的一元二次方程(a＋1)x2－x＋a2－2a－2＝0有一根是1，求a的值．

    a＝2． 【解析】试题分析：将方程的根代入得到有关a的方程求解即可确定a的值，注意利用一元二次方程的定义舍去不合题意的根，从而确定a的值． 【解析】 将x=1代入， 得：（a+1）2﹣1+a2﹣2a﹣2=0， 解得：a1=﹣1，a2=2． ∵a+1≠0， ∴a≠﹣1， ∴a=2．

    查看答案和解析>>

    科目：初中数学 来源：内蒙古赤峰市翁牛特旗2018届九年级上学期期末考试数学试卷 题型：解答题

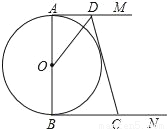
    如图，AB是⊙O的直径，AM、BN分别与⊙O相切于点A、B，CD交AM、BN于点D、C，DO平分∠ADC．

    （1）求证：CD是⊙O的切线；

    （2）设AD=4，AB=x （x＞0），BC=y （y＞0）．求y关于x的函数解析式．

    （1）详见解析；（2）y=x2． 【解析】（1）证明：过O做OE⊥CD于点E， 则∠OED＝90° ∵⊙O与AM相切于点A ∴∠OAD＝90° ∵OD平分∠ADE ∴∠ADO＝∠EDO ∵OD＝OD ∴△OAD≌△OED ∴OE＝OA ∵OA是⊙O的半径 ∴OE是⊙O的半径 ∴CD是⊙O的切线 （2）过点D做DF⊥BC于...

    查看答案和解析>>

    同步练习册答案