
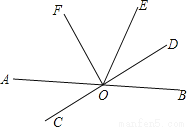
��ͼ��ֱ��AB��CD�ཻ�ڵ�O��ODƽ�֡�BOE����FOD=90�㣬��OF�ǡ�AOE��ƽ���������㲹������С��Ľ����̣�
̽����
��1������BOE=70��ʱ����BOD=��DOE=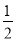 ��70��=35�㣬��EOF=90�㩁��DOE= �㣬����AOF+��FOD+��BOD=180�㣬���ԡ�AOF+��BOD=180�㩁��FOD=90�㣬���ԡ�AOF=90�㩁��BOD= �㣬���ԡ�EOF=��AOF��OF�ǡ�AOE��ƽ���ߣ�
��70��=35�㣬��EOF=90�㩁��DOE= �㣬����AOF+��FOD+��BOD=180�㣬���ԡ�AOF+��BOD=180�㩁��FOD=90�㣬���ԡ�AOF=90�㩁��BOD= �㣬���ԡ�EOF=��AOF��OF�ǡ�AOE��ƽ���ߣ�
��2���ο����棨1���Ľ����̣�����֤��������BOEΪ����Ƕ�ʱ��OF�ǡ�AOE��ƽ���ߣ�
��3��ֱ��д�����AOF��������нǣ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��ɽ��ʡ��ׯ��������2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��ͼ�Ǽס���������ijʱ���ٶ���ʱ��仯��ͼ�����н��۴�����ǣ�������
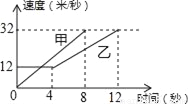
A. ��ǰ4����ʻ��·��Ϊ48��
B. ��0��8���ڼ��ٶ�ÿ������4��/��
C. ��������3��ʱ��ʻ��·�����
D. ��4��8���ڼ��ٶȶ������ҵ��ٶ�
C �����������������A������ͼ��ɵã���ǰ4����ʻ��·��Ϊ12��4=48�ף���ȷ�� B������ͼ��ã���0��8���ڼ��ٶ�ÿ������4����/����ȷ�� C������ͼ��ɵ���������3��ʱ��ʻ��·�̲���ȣ��ʱ�ѡ����� D����4��8���ڼ��ٶȶ������ҵ��ٶȣ���ȷ�� ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶12���¿���ѧ�Ծ� ���ͣ������
ѧУΪ������������д������������ѧ����������ʦ���̵깺��ij�ֽ�Ʒ����������ͼ��ʾ�Ĺ��ڸý�Ʒ��������Ϣ��
������� | ���ۼ۸� |
������30�� | ����40Ԫ |
����30�� | ÿ����1������������г������۽���0.5Ԫ�������۲��õ���30Ԫ |
����1400Ԫ����˽�Ʒ��������ʦ����ý�Ʒ�ļ�����
����ʦ����ý�Ʒ�ļ���Ϊ40���� ��������������������жϹ���ļ���������30���蹺����x������ʾ��ÿ����Ʒ�ļ۸����ó�������Ʒ����Ǯ����������Ǯ����1400Ԫ������������𰸣� ��������� �������� ��30��40��1200��1400�� �ཱƷ��������30���� ������Ϊx������ÿ����Ʒ�ļ۸�Ϊ��[40��(x��30)��0.5]Ԫ�� ��������ɵã� x[...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
��һ������������ƽ��2����λ��õ���y=2x2�ĺ���ͼ���������������ǣ� ��
A��y=2x2+2 B��y=2x2��2
C��y=2��x��2��2 D��y=2��x+2��2
C�� �������� ������������������ߵ�ƽ�ƹ��ɿɵ�,��һ������������ƽ��2����λ��õ���y=2x2�ĺ���ͼ����������������y=2��x��2��2 ,�ʴ�ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
һԪ���η���x2��6x��3��0������Ϊx1��x2���� x1��x2��ֵΪ�� ��
A. ��3 B. 6 C. 3 D. ��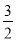
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��̰���ѧ�Ծ���C���� ���ͣ������
��֪123456789101112��997998999������������1��999������ɵ�һ�������ڸ����д�����������2013λ�ϵ�����Ϊ_____��
7�� ��������������֪�ó���2013�������ǵ�608��3λ���ĵ�3λ�������ó����ɣ� �������� �߹���9��1λ����90��2λ����900��3λ�� ��2013��9��180=1824�� ��=608�� �ߴ�608�Ǽ�99��ĵ�608���� �������707������λ��7 �ʴ�����������2013λ�ϵ�����Ϊ7�� �ʴ�Ϊ��7���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��̰���ѧ�Ծ���C���� ���ͣ���ѡ��
���a3=��27��b2=16����ab��ֵΪ�� ��
A.��12 B.12 C.1��7 D.��12
D �������� ����������Ƚ��п�������õ�a=��3��b=��4��Ȼ��ֱ����ab���м��㼴�ɣ� �������� ��a3=��27��b2=16�� ��a=��3��b=��4�� ��ab=��3��4=��12��ab=��3������4��=12�� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����������2018����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ������
���κ���y=��x2+2x��3�����䷽����Ϊy=a��x��h��2+k����ʽΪ_____��
y=����x��1��2��2 ���������ߣ� ���Ϊ�� .�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶�˽̰���ѧ�Ծ���C���� ���ͣ������
��һ��ֱ����������A��B��C�����ۿڣ�A��B�������30ǧ�ף�B��C�������90ǧ��.�ס�������ͬʱ�ֱ��A��B�ۿڳ�������ֱ������ʻ��C�ۣ����մﵽC�ۣ���0.5Сʱ����B�ۣ���ʱ�������15ǧ��.
��1���״���ʱ���ң���ʱ����C�۶�Զ��
��2����ʱ�����������10ǧ��.
��1��1Сʱ�����ң���ʱ����C��60ǧ�ף���2�� ��. �������������������1���ȸ���������üס����������ٶȣ�Ȼ����ݼ״���·�̱��Ҵ���·�̶�30ǧ���з�����⼴�ɣ� ��2����Ϊ�����ҵĺ���ͼ����ҵ�ǰ����������з�����⼴�ɣ� ���������(1)��0.5Сʱ����B�ۣ���ʱ�������15ǧ�ף� �������30ǧ�ף� ��״����ٶ�Ϊ60ǧ��/Сʱ���ҵ��ٶ�Ϊ30ǧ��/Сʱ. ...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com