
国庆长假期间,以生态休闲为特色的德阳市近郊游备受青睐.假期各主要景点人气爆棚,据市旅游局统计,本次长假共实现旅游收入5610万元.将这一数据用科学记数法表示为( )
A. 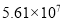 B.
B. 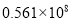 C.
C. 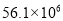 D.
D. 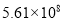
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
解分式方程:(1)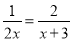 (2)
(2) 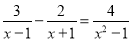
查看答案和解析>>
科目:初中数学 来源:北京市海淀区2017-2018学年第一学期七年级期末考试数学参考样题 题型:单选题
下列是一元一次方程的是( )
A. 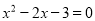 B.
B. 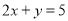 C.
C. 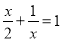 D.
D. 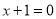
查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季七年级期末考试 题型:填空题
这个平面展开图还原成立体图形是 ____________.
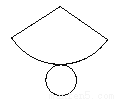
查看答案和解析>>
科目:初中数学 来源:四川省江县初中2016年秋季七年级期末考试 题型:单选题
下面计算步骤正确的是( )
A. 由2(2x-1)-3(x-3)=1,变形得4x-2-3x-9=1 .
B. 由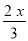 =1+
=1+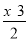 ,变形得2(2-x)=1+3(x-3) .
,变形得2(2-x)=1+3(x-3) .
C. 若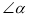 的补角是它的3倍,则
的补角是它的3倍,则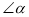 = 22.5°.
= 22.5°.
D. 若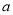 与
与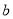 互为倒数,则-
互为倒数,则-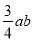 =-
=-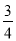 .
.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期末检测题(一) 题型:解答题
如图,某市为方便相距2 km的A,B两处居民区的交往,修筑一条笔直的公路(即图中的线段AB),经测量,在A处的北偏东60°方向、B处北偏西45°方向的C处有一半径为0.7 km的圆形公园,问计划修筑的公路会不会穿过公园?为什么?
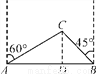
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期末检测题(一) 题型:填空题
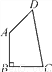
如图,在四边形ABCD中,AB,BC,CD,DA的长分别为2,2,2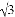 ,2,且AB⊥BC,则∠BAD的度数等于____.
,2,且AB⊥BC,则∠BAD的度数等于____.
查看答案和解析>>
科目:初中数学 来源:贵州省遵义市2018届九年级(上)第一次月考数学试卷 题型:解答题
已知二次函数y=x2+bx+c的图象经过点(0,2)和(1,﹣1),求图象的顶点坐标和对称轴.
顶点坐标是(2,﹣2),对称轴是直线x=2. 【解析】试题分析: 要求二次函数的顶点坐标和对称轴,需要得到二次函数的解析式. 因为条件中的两点均在该二次函数的图象上,所以这两点的横纵坐标应该满足该二次函数的解析式. 将相应坐标代入解析式就得到了一个关于待定系数b与c的二元一次方程组,进而容易求得该二次函数的解析式. 由于该解析式符合二次函数的一般形式,可以通过相关公式求得顶点坐标和对称...查看答案和解析>>
科目:初中数学 来源:湖北省2017-2018学年九年级上期元月调考数学试卷(2) 题型:单选题
在一个不透明的袋子里,有2个白球和2个红球,它们只有颜色上的区别,从袋子里随机摸出一个球记下颜色放回,再随机地摸出一个球,则两次都摸到白球的概率为( )
A.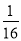 B.
B.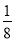 C.
C.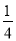 D.
D.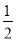
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com