
��֪���κ���y=x2+bx+c��ͼ���㣨0��2���ͣ�1����1������ͼ��Ķ�������ͶԳ��ᣮ
���������ǣ�2����2�����Գ�����ֱ��x=2�� ����������������� Ҫ����κ����Ķ�������ͶԳ��ᣬ��Ҫ�õ����κ����Ľ���ʽ. ��Ϊ�����е�������ڸö��κ�����ͼ���ϣ�����������ĺ�������Ӧ������ö��κ����Ľ���ʽ. ����Ӧ����������ʽ�͵õ���һ�����ڴ���ϵ��b��c�Ķ�Ԫһ�η����飬����������øö��κ����Ľ���ʽ. ���ڸý���ʽ���϶��κ�����һ����ʽ������ͨ����ع�ʽ��ö�������ͶԳ�...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�������к�����2017-2018ѧ���һѧ�����꼶��ĩ������ѧ�ο����� ���ͣ������
�涨ͼ�� ��ʾ����
��ʾ����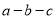 ��ͼ��
��ͼ�� ��ʾ����
��ʾ����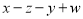 .��
.�� +
+ 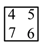 =________________��ֱ��д���𰸣���
=________________��ֱ��д���𰸣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ���س���2016���^���꼶��ĩ���� ���ͣ���ѡ��
���쳤���ڼ䣬����̬����Ϊ��ɫ�ĵ����н����α������������ڸ���Ҫ������������������ξ�ͳ�ƣ����γ��ٹ�ʵ����������5610��Ԫ������һ�����ÿ�ѧ��������ʾΪ�� ��
A. 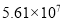 B.
B. 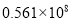 C.
C. 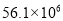 D.
D. 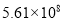
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ�˽̰棩����ĩ�����(һ) ���ͣ���ѡ��
��ͼ�����ı���ABCD�У���ABC��90�㣬AD��BC��AE��CD��BC�ڵ�E��AEƽ�֡�BAC��AO��CO��AD��DC��2��������ۣ���AC��2AB����AB��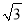 ����S��ADC��2S��ABE����BO��AE.������ȷ����( )
����S��ADC��2S��ABE����BO��AE.������ȷ����( )
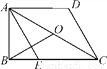
A. 1�� B. 2�� C. 3�� D. 4��
D �������������������AD��BC��AE��CD�� ���ı���AECD��ƽ���ı��Σ� ��AD��DC�� ���ı���AECD�����Σ� ��AE��EC��CD��AD��2�� ���2����3�� �ߡ�1����2�� ���1����2����3�� �ߡ�ABC��90�㣬 ���1����2����3��90�㣬 ���1����2����3��30�㣬 ��BE��AE��1��AC��2AB������...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ�²ᣨ�˽̰棩����ĩ�����(һ) ���ͣ���ѡ��
ijר����רӪijƷ�Ƶij�������������һ���в�ͬ����ij����������ͳ�����£�
���� | 39 | 40 | 41 | 42 | 43 |
ƽ��ÿ����������/�� | 10 | 12 | 20 | 12 | 12 |
�õ����������ܽ���ʱ������һЩ41��ij�����Ӱ��õ������ߵ�ͳ�����ǣ� ��
A. ƽ���� B. ���� C. ���� D. ��λ��
C ��������������������������������г��ִ�������������Ӱ��õ������ߵ�ͳ������������ ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ������
��������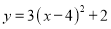 ����ƽ��1����λ���ȣ�������ƽ��3����λ���ȣ�ƽ�ƺ������ߵĽ���ʽ�� ��
����ƽ��1����λ���ȣ�������ƽ��3����λ���ȣ�ƽ�ƺ������ߵĽ���ʽ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶���ϣ���һ���¿���ѧ�Ծ� ���ͣ���ѡ��
��x=2����x��һԪ���η���x2��ax+2=0��һ��������a��ֵΪ�� ��
A��3 B����3 C��1 D����1
A �������� ������������̵ĸ�������ʹ���̵�����������ȵ�δ֪����ֵ�������x=2�������x��һԪ���η���x2��ax+2=0���Ϳ������a��ֵ�� �������� ��x=2����x2��ax+2=0���� 22��2a+2=0�� ���a=3�� ��ѡ��A���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶����Ԫ�µ�����ѧ�Ծ���2�� ���ͣ������
�����Ĵ�����װ�д�С���ʵ���ȫ��ͬ��2�������2������
(1) �ȴӴ���Ͷ��1�����Żأ���Ͼ��Ⱥ�������1�������һ���������ڶ�����������ĸ���ΪP1Ϊ__________��
(2) ����һ�δӴ���������1����Żأ��ڶ���������1����������������������1�������1������ĸ���P2�Ƕ���?(���û�����ͼ���б�����������
��1������2��. �������������������1��������ͼ�ó����еȿ��ܵ���������ҳ�����������������������������ĸ��ʣ� ��2���ɱ�Ȼ�¼��Ķ����֪�����Ĵ�����װ�Ķ��Ǻ��Ӵ������������һ�����Ǻ�����¼�Ϊ����Ȼ�¼������ܳ���������m��ֵ��������� ��2���б��ó����еȿ��ܵ���������ҳ���������������ɫ��ͬ��������������������ĸ��ʣ� �����������1������״ͼ�ã� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������з�̨��2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ���WORD�棩 ���ͣ���ѡ��
��� ����ô���ݵ�ʽ���������б�����ȷ���ǣ�������
����ô���ݵ�ʽ���������б�����ȷ���ǣ�������
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com